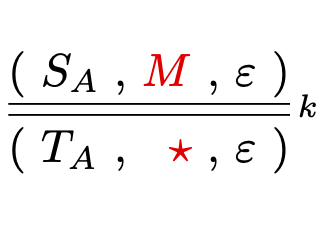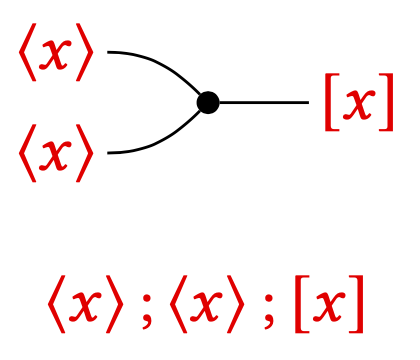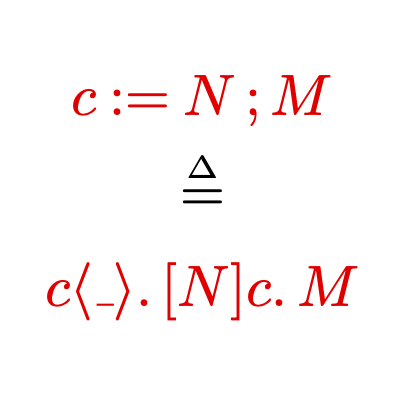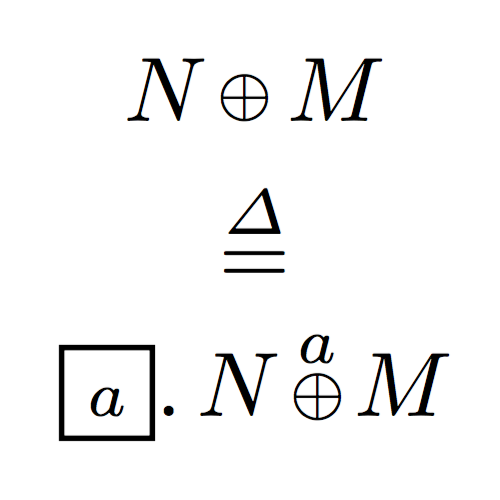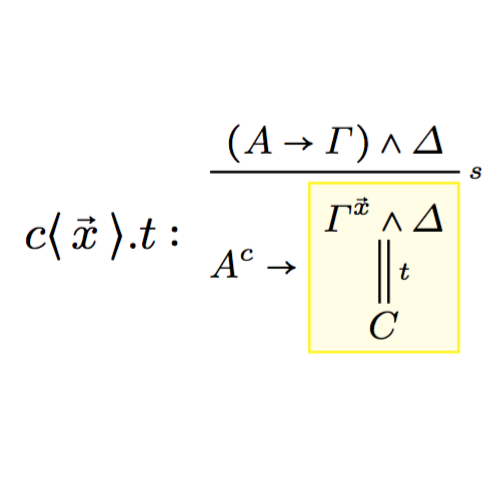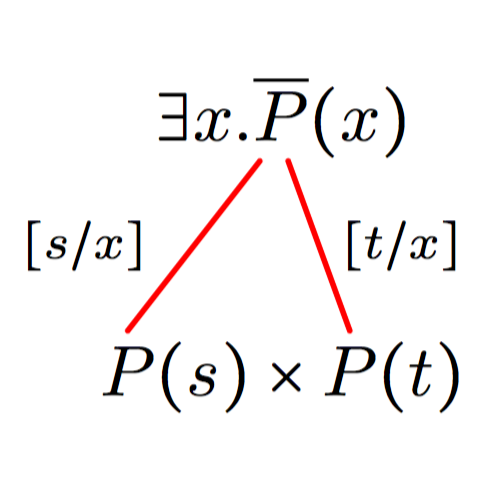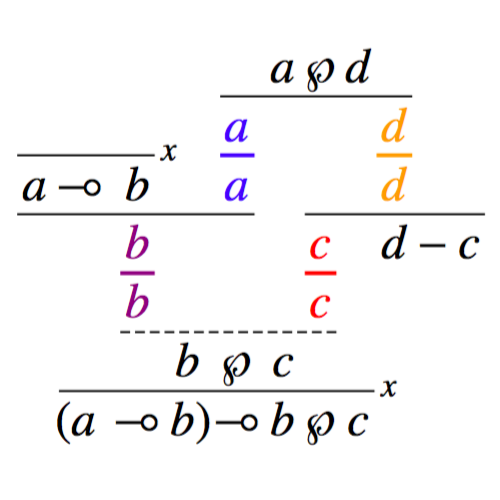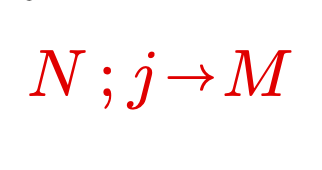Dr Willem Heijltjes

I'm a Senior Lecturer and Prize Fellow in the Mathematical Foundations group, Department of Computer Science, University of Bath.

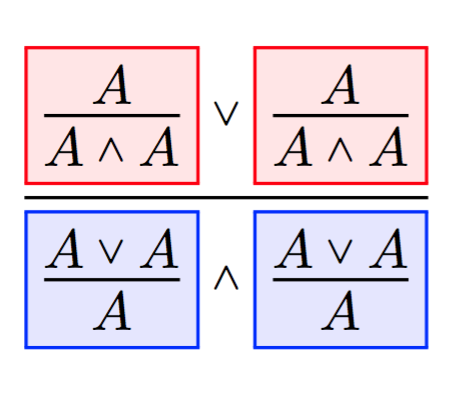
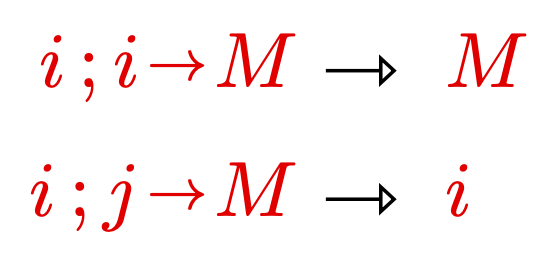
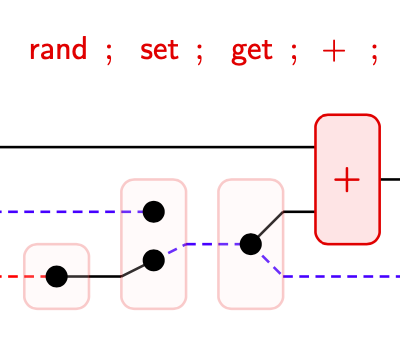
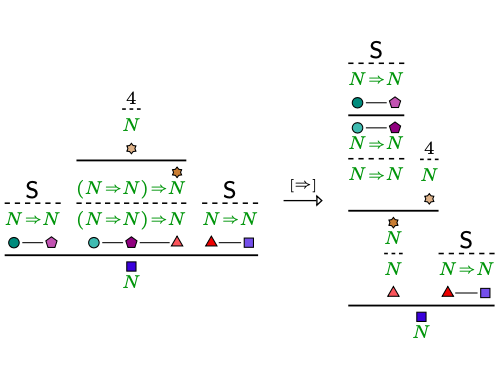
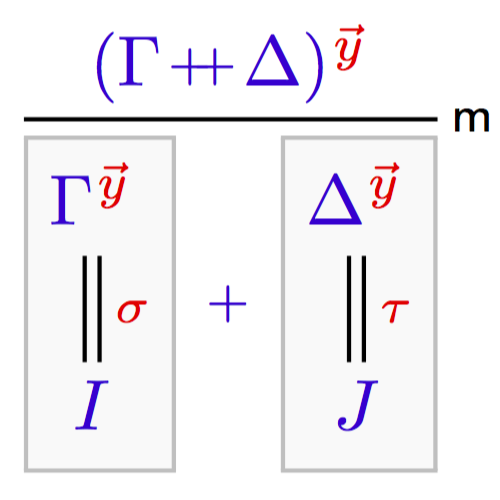
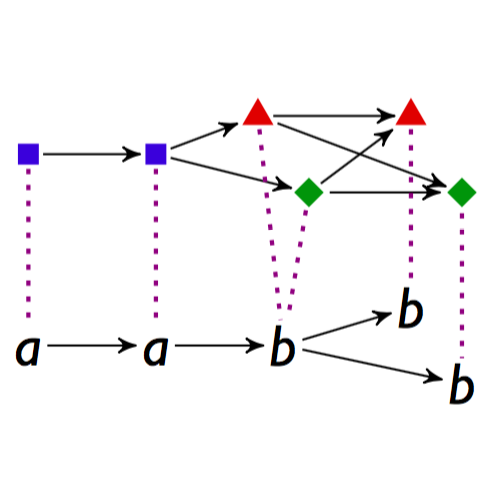
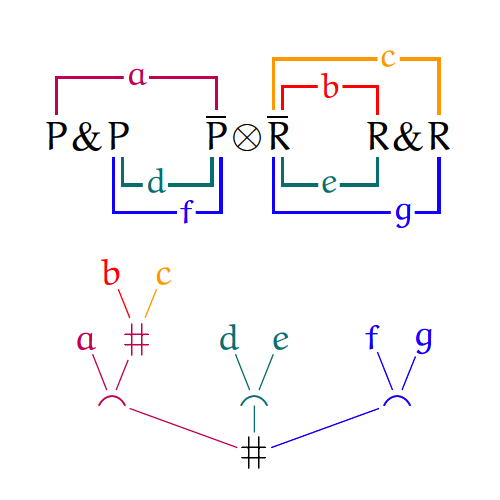
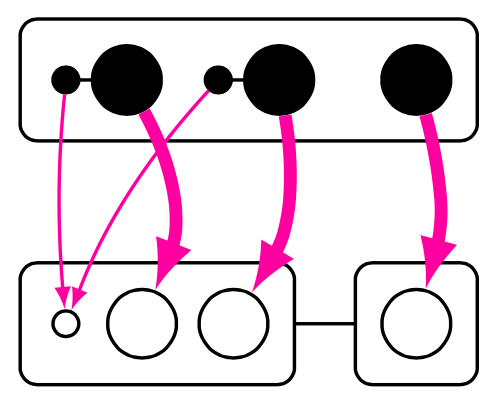
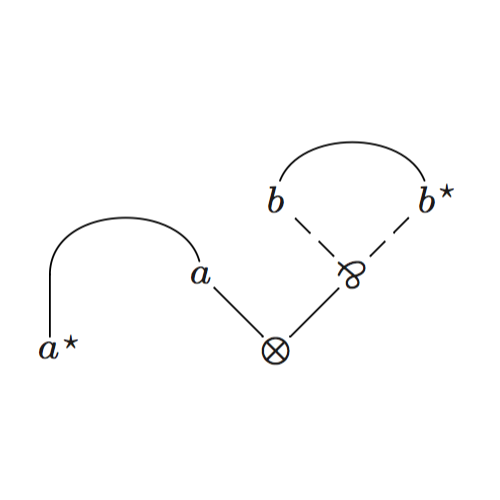
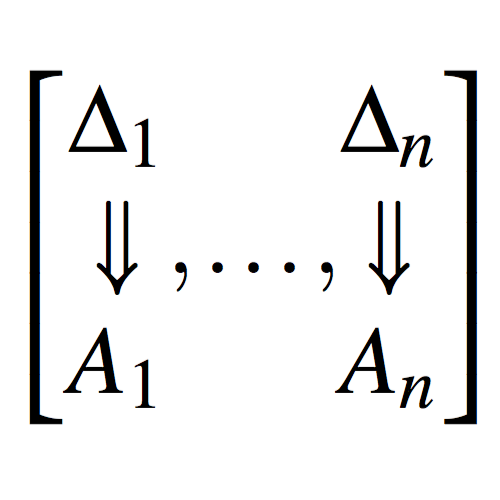
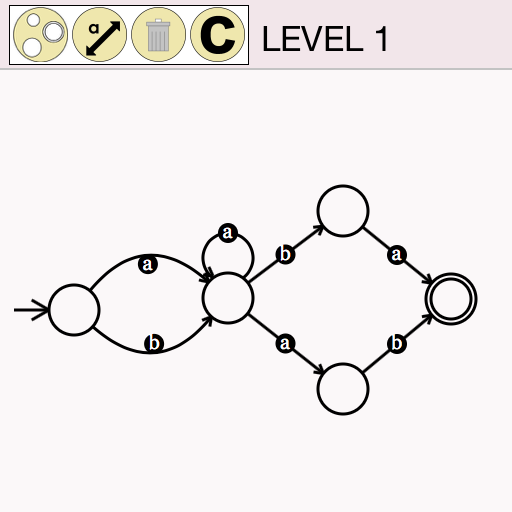
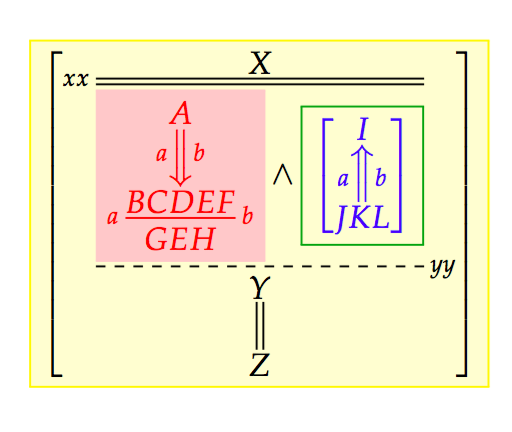
My research is in the area of structural proof theory, where I investigate the fundamental structure of proofs and their application as type systems. I have worked on canonical graphical representations of proof (commonly known as proof nets), on computational interpretations of deep-inference proof theory, and on typed calculi for computational effects and imperative programming.

Typed Lambda-Calculi with Sharing and Unsharing

EPSRC project EP/R029121/1 | January 2019 - July 2022

In this project we investigate the computational potential of deep-inference proof theory, via the Curry-Howard correspondence between intuitionistic logic and simple types for the lambda-calculus.

Project page

Simple types for probabilistic termination

Willem Heijltjes and Georgina Majury

CSL 2025

We present a system of simple types to give lower bounds on the probability of termination of probabilistic lambda-terms. The intuition is to take simple types and view the base type as signifying successful termination. Our type system then replaces base types with probabilities (rationals between zero and one).

PDF

The Relational Machine Calculus

Chris Barrett, Daniel Castle, and Willem Heijltjes

LICS 2024

We extend the first-order Functional Machine Calculus, a language for Cartesian categories, to a model of relational computation. The Relational Machine Calculus (RMC) introduces non-determinism, iteration, and unification, making it a Kleene algebra that operates as a stack calculus with perfect duality between push and pop. The RMC naturally embeds various first-order models of computation, including automata, Turing machines, Petri nets, interaction nets, and logic programming.

PDF | arXiv:2405.10801

The Functional Machine Calculus II: Semantics

Chris Barrett, Willem Heijltjes, and Guy McCusker

CSL 2023

We investigate the semantics of the Functional Machine Calculus, introduced in the paper below. We give a domain-theoretic account of the untyped calculus, and for the typed calculus a Gandy-style proof of strong normalization and a categorical account as a Cartesian closed category.

PDF | arXiv:2211.13140 | DOI: 10.4230/LIPIcs.CSL.2023.10

The Functional Machine Calculus

Willem Heijltjes

MFPS 2022

The Functional Machine Calculus (FMC) is a new model of effectful functional computation. Viewing the lambda-calculus as an instruction language for a simple stack machine in the style of Krivine, it is extended firstly with multiple stacks, to model the effects of state, I/O, probabilities, and non-determinism; and secondly with sequential composition, to model strategies including call–by–name, call–by–value, and call–by–push–value.

PDF | arXiv:2212.08177 | DOI: 10.46298/entics.10513 | Talk (HOPE'21)

Normalization Without Syntax

Willem Heijltjes, Dominic Hughes, and Lutz Straßburger

FSCD 2022

We present a simple method for normalization of intuitionistic combinatorial proofs. Rather than including a cut construct inside the calculus, or computing the result directly by combinatorial manipulation, we build a tree with combinatorial proofs as nodes and cuts as edges. Normalization may then follow the standard reduction rules of the sequent calculus, but in a setting that is free of permutations.

PDF | DOI: 10.4230/LIPIcs.FSCD.2022.19 | Talk

A deep quantitative type system

Giulio Guerrieri, Willem Heijltjes, and Joe Paulus

CSL 2021

We investigate intersection types and resource lambda-calculi from the perspective of deep-inference proof theory. We give a single underlying type system that is parameterized in a choice of algebraic laws to represent different flavours of quantitative reasoning about lambda-calculi.

PDF | DOI: 10.4230/LIPIcs.CSL.2021.24 | Talk

Decomposing probabilistic lambda-calculi

Ugo Dal Lago, Giulio Guerrieri, and Willem Heijltjes

FoSSaCS 2020

Probabilistic lambda-calculi are generally non-confluent, with call-by-name and call-by-value providing different results. Via a decomposition of the usual probabilistic sum into a generator that generates a probabilistic event and a choice that evaluates differently depending on a given event, we capture both reduction regimes, as well as many intermediate ones, in a single, confluent probabilistic lambda-calculus.

PDF | DOI: 10.1007/978-3-030-45231-5_8 | Long version

Spinal atomic lambda-calculus

David Sherratt, Willem Heijltjes, Tom Gundersen, and Michel Parigot

FoSSaCS 2020

We investigate the computational side of the switch rule of deep-inference proof theory, and link it to end-of-scope operators and director strings in lambda-calculus. We use this to extend the atomic lambda-calculus, obtaining a more refined version of full laziness, spine duplication.

PDF | DOI: 10.1007/978-3-030-45231-5_30

Proof nets for first-order additive linear logic

Willem Heijltjes, Dominic Hughes, and Lutz Straßburger

FSCD 2019

We give two flavours of proof nets for additive linear logic with first-order quantification: one where existential witnesses are recorded via explicit substitutions, attached to axiom links; and one where witness information is omitted, and reconstructed by unification.

PDF | DOI: 10.4230/LIPIcs.FSCD.2019.22

Intuitionistic proofs without syntax

Willem Heijltjes, Dominic Hughes, and Lutz Straßburger

LICS 2019

We extend Hughes's classical Combinatorial Proofs to intuitionistic logic. We obtain a purely geometric, concrete semantics that has polynomial full completeness (no size explosion when translating from sequent calculus) and local canonicity (all non-duplicating permutations are factored out).

PDF | DOI: 10.1109/LICS.2019.8785827

Proof nets for bi-intuitionistic linear logic

Gianluigi Bellin and Willem Heijltjes

FSCD 2018

Bi-intuitionistic linear logic (BILL) combines the tensor and linear implication of intuitionistic linear logic (ILL) with their duals, par and subtraction, relating tensor and par through a linear distributivity. We give canonical proof nets for this proof-theoretically challenging logic, with correctness through both contractibility and switching.

PDF | DOI: 10.4230/LIPIcs.FSCD.2018.10

Conflict nets: Efficient locally canonical MALL proof nets

Dominic Hughes and Willem Heijltjes

LICS 2016

We give a new notion of proof net for Multiplicative-Additive Linear Logic, that strikes a subtle balance between efficiency and canonicity. Conflict nets are canonical for all local rule commutations, which are those that do not incur a global duplication. As a consequence they have linear size compared to sequent proofs, avoiding the exponential growth of Hughes and Van Glabbeek's Slice Nets.

PDF | DOI: 10.1145/2933575.2934559

Proof equivalence in MLL is PSPACE-complete

Willem Heijltjes and Robin Houston

Logical Methods in Computer Science 12(1) 2016

Proof equivalence in MLL with units is shown to be PSPACE-complete, by a reduction from the graphical formalism called Non-Deterministic Constraint Logic. This effectively rules out a satisfactory notion of proof net with units, as such a notion would constitute a tractable decision algorithm for proof equivalence.

PDF | arXiv | DOI: 10.2168/LMCS-12(1:2)2016

Proof nets and semi-star-autonomous categories

Willem Heijltjes and Lutz Straßburger

Mathematical Structures in Computer Science 26(5):789-828 (2016)

We consider a notion of semi-star-autonomous category: star-autonomous categories without units, corresponding to Girard's proof nets for MLL. (Available online since November 2014.)

PDF | DOI: 10.1017/S0960129514000395

Complexity bounds for sum-product logic
via additive proof nets and Petri nets

Willem Heijltjes and Dominic Hughes

LICS 2015

We give an effective correctness criterion for additive proof nets, which is naturally expressed in Petri nets, and is the equivalent of Danos contractibility for MLL. In addition we give simple proof search algorithms for additive linear logic with and without units and an effective correctness algorithm for additive proof nets with units, and we show that first-order additive linear logic is NP-complete.

PDF | DOI: 10.1109/LICS.2015.18

No proof nets for MLL with units:
Proof equivalence in MLL is PSPACE-complete

Willem Heijltjes and Robin Houston

CSL-LICS 2014

Proof equivalence in MLL with units is shown to be PSPACE-complete, by a reduction from the graphical formalism called Non-Deterministic Constraint Logic. This effectively rules out a satisfactory notion of proof net with units, as such a notion would constitute a tractable decision algorithm for proof equivalence. (Superseded by the journal version Proof equivalence in MLL is PSPACE-complete.)

PDF | DOI: 10.1145/2603088.2603126

A Proof of Strong Normalisation for the Typed Atomic Lambda-Calculus

Tom Gundersen, Willem Heijltjes, and Michel Parigot

LPAR 2013

The atomic lambda-calculus is a typeable lambda-calculus with explicit sharing, which originates in a Curry-Howard interpretation of a deep-inference system for intuitionistic logic. In this paper we prove strong normalization of the typed atomic lambda-calculus using Tait's reducibility method.

PDF | DOI: 10.1007/978-3-642-45221-5_24

Atomic lambda-calculus:
a typed lambda-calculus with explicit sharing

Tom Gundersen, Willem Heijltjes, and Michel Parigot

LICS 2013

The atomic lambda-calculus is a typeable lambda-calculus with explicit sharing, based on a Curry-Howard-style interpretation of the deep inference proof formalism. Duplication of subterms during reduction proceeds atomically, i.e. on individual constructors, similar to optimal graph reduction in the style of Lamping. The calculus preserves strong normalisation and achieves fully lazy sharing.

PDF | DOI: 10.1109/LICS.2013.37

Proof nets for additive linear logic with units

Willem Heijltjes

LICS 2011

The paper describes canonical proof nets for additive linear logic, or sum-product logic, the internal language of categories with free finite products and co-products. Starting from existing proof nets, which disregard the unit laws, canonical nets are obtained by a simple rewriting algorithm, for which a substantial correctness proof is provided.

Awarded the LICS 2011 Kleene award for best student paper

PDF | DOI: 10.1109/LICS.2011.9

Classical Proof Forestry

Willem Heijltjes

Annals of Pure and Applied Logic 161 (11), pp. 1346-1366, 2010

The paper investigates cut-elimination in classical proof forests, a proof formalism for first-order classical logic based on Herbrand's Theorem and backtracking games in the style of Coquand. Cut-free classical proof forests were described by Miller, and are called Expansion Tree Proofs.

Preprint | DOI: 10.1016/j.apal.2010.04.006

The Functional Machine Calculus III: Choice

Willem Heijltjes

Mathematical Foundations of Programming Semantics (MFPS) 2024

PDF | arXiv:2411.04615

The Functional Machine Calculus

Willem Heijltjes

Higher-Order Programming with Effecs (HOPE) 2021

Superseded by The Functional Machine Calculus (MFPS 2022).

PDF | Talk

Deep-Inference Intersection Types

Joe Paulus and Willem Heijltjes

Twenty Years of Deep Inference (TYDI) 2018

Superseded by A deep quantitative type system.

PDF

Un Lambda-Calcul Atomique

Tom Gundersen, Willem Heijltjes et Michel Parigot

Journées Francophones des Langages Applicatifs (JFLA) 2013

Superseded by Atomic lambda-calculus: a typed lambda-calculus with explicit sharing.

Français | English

Proof Forests with Cut Based on Herbrand's Theorem

Willem Heijltjes

Classical Logic & Computation (CL&C) 2008

Superseded by Classical Proof Forestry.

PDF

Georgi Majury

PhD

Homepage

Chris Barrett

PhD | Successfully defended December 2022

Doctoral thesis: On the Simply-Typed Functional Machine Calculus: Categorical Semantics and Strong Normalisation

Homepage

David Sherratt

PhD | Successfully defended May 2019

Doctoral thesis: A lambda-calculus that achieves full laziness with spine duplication

Homepage

Dr Fanny He

PhD | Successfully defended April 2018

Doctoral thesis: The Atomic Lambda-Mu Calculus

Homepage

Logic Games

A collection of educational computer games for logic in computer science, made by final-year undergraduate students.

Logic Games

Open Deduction LaTeX macros

A LaTeX package for drawing derivations in open deduction.

opendeduction.sty | Manual

Paper plane

Folding instructions for a good-looking and reasonably-flying paper airplane.

PDF

Senior Lecturer

December 2019 - present

Lecturer

November 2014 - November 2019

Prize Fellow

November 2012 - October 2014

Department of Computer Science
University of Bath

Postdoctoral researcher

October 2011 - October 2012

Team Parsifal | LIX | École Polytechnique

PhD in Theoretical Computer Science

November 2011 (viva), June 2012 (graduation)

Laboratory for the Foundations of Computer Science (LFCS)
School of Informatics | University of Edinburgh

Doctoral thesis: Graphical Representation of Canonical Proof: Two case studies

Thesis advisor: Professor Alex Simpson

Master of Science in Cognitive Artificial Intelligence

March 2007

Department of Philosophy | Utrecht University

Master's thesis: Graph Rewriting for Natural Deduction and the Proper Treatment of Variables

Winner of the Cognitive Artificial Intelligence thesis award 2007, Department of Philosophy, Utrecht University

Thesis advisors: Professor Albert Visser and Professor Vincent van Oostrom