Chapter 12 The heat equation on a disc revisited
12.1 The radial eigenvalue problem for the disc
We further investigate the eigenvalue equation for the \(R\)-equation in polar coordinates, i.e. (5.4) and (5.5) which we repeat here:
\[ R''+\frac {1}{r}R'-\frac {\sigma ^2}{r^2}R=\lambda R,\qquad R(b)=0. \]
We will have \(\lambda \leq 0\) (a similar argument to that in Chapter 5 for the \(\Theta \) equation works here) and we write \(\lambda =-\eta ^2\) with \(\eta \geq 0\). We therefore consider (now using the standard Sturm–Liouville notation \(u\) and \(x\) instead of \(R\) and \(r\))
\(\seteqnumber{0}{12.}{0}\)\begin{equation} \label {eq:Besselparametric} x^2u''+xu'+(\eta ^2 x^2-\sigma ^2)u=0. \end{equation}
This is called the parametric form of Bessel’s equation of order \(\sigma \) (and parameter \(\eta \)).
Let \(J_\sigma \) be the Bessel function of order \(\sigma \) from Chapter 11. Define \(u(x):=J_\sigma (\eta x)\). We then have
\[ u'(x)=\eta J_\sigma '(\eta x),\qquad u''(x)=\eta ^2J_\sigma ''(\eta x). \]
Hence
\[ x^2u''+xu'+(\eta ^2x^2-\sigma ^2)u =x^2\eta ^2J_\sigma ''(\eta x)+x\eta J_\sigma '(\eta x)+(\eta ^2x^2-\sigma ^2)J_\sigma (\eta x) =0, \]
where in the last step we use that \(z^2J_\sigma ''(z)+zJ_\sigma '(z)+(z^2-\sigma ^2)J_\sigma (z)=0\) with \(z=\eta x\) (i.e. that \(J_\sigma \) satisfies the Bessel equation of order \(\sigma \)). Hence this scaled version of the Bessel function satisfies the parametric form of Bessel’s equation.
To satisfy the boundary condition \(u(\b )=0\) we must have
\[ J_\sigma (\eta \b )=0. \]
This means that \(\eta \b \) must be a zero of the Bessel function \(J_\sigma \). The Bessel functions have countably many positive zeros; we denote by \(z_{\sigma n}\) the \(n\)-th zero of \(J_\sigma \) (here \(n\in \mN \)). We then have
\[ \eta =\frac {z_{\sigma n}}{\b }, \]
so that the eigenvalues are
\[ \lambda _n=-\left (\frac {z_{\sigma n}}{\b }\right )^2,\qquad n\in \mN , \]
and the eigenfunctions are
\[ u_n(x)=J_\sigma \left (\frac {z_{\sigma n}}{\b }x\right ),\qquad n\in \mN . \]
-
Remark. We note that \(J_\sigma \in L^2(0,\b ;x)\) and that for \(\sigma <1\) it additionally satisfies the boundary condition
\[ \lim _{x\downarrow 0} J_\sigma '(x)x^{\sigma +1}-J_\sigma (x)\sigma x^\sigma , \]
which we obtained in Example 9.7 from \(v(x)=x^\sigma \). This is shown as follows.
We can write the Bessel function of order \(\sigma \) as \(x^\sigma \) times a power series which converges on \(\mC \) and therefore it is continuous for all \(\sigma \geq 0\). In particular, it is in \(L^2(0,\b ;x)\) so that for \(\sigma \geq 1\) we have found our unique linearly independent solution in this space. We write \(J_\sigma (x)=x^\sigma f(x)\) where \(f\) is represented by the power series calculated in Chapter 11. Using the product rule we have
\[ J_\sigma '(x)=x^\sigma f'(x)+\sigma x^{\sigma -1}f(x), \]
so that
\[ J_\sigma '(x)x^{\sigma +1}-J_\sigma (x)\sigma x^\sigma =x^{2\sigma +1}f'(x)+x^{2\sigma }\sigma f(x)-f(x)\sigma x^{2\sigma }=x^{2\sigma +1}f'(x). \]
We in particular have
\[ \lim _{x\downarrow 0} J_\sigma '(x)x^{\sigma +1}-J_\sigma (x)\sigma x^\sigma =\lim _{x\downarrow 0}x^{2\sigma +1}f'(x) =0. \]
Therefore, the eigenfunctions \(u_n\) that we have above are the “correct” ones (and ones based on \(Y_\sigma \) are “incorrect”).
12.2 The heat equation on the disc: solution
We recall from Chapter 5 the eigenvalues and normalized eigenfunctions for the \(\Theta \) equation in polar coordinates as (for \(k=0\) the eigenvalue has multiplicity 1 and for \(k\in \mN \) it has multiplicity 2):
\(\seteqnumber{0}{12.}{1}\)\begin{equation} \label {eq:Thetak} \lambda ^\Theta _k=-k^2,\qquad \frac {1}{\sqrt {2\pi }},\quad \frac {1}{\sqrt {\pi }}\sin (k\theta ),\quad \frac {1}{\sqrt {\pi }}\cos (k\theta ). \end{equation}
The \(R\) equation in polar coordinates then is the parametric form of Bessel’s equation of order \(k\). We therefore obtain the eigenvalues and normalized eigenfunctions (here \(k\in \mN _0\) as above and \(n\in \mN \))
\[ \lambda _{kn}=-\left (\frac {z_{kn}}{b}\right )^2,\qquad u_{kn}(\theta ,r)=\Theta _k(\theta )R_{kn}(r), \]
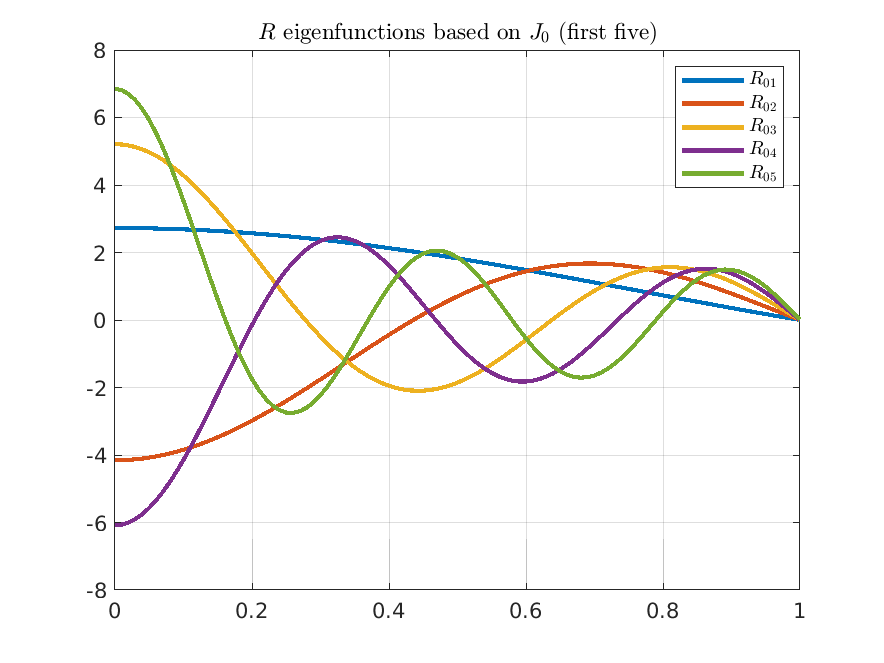
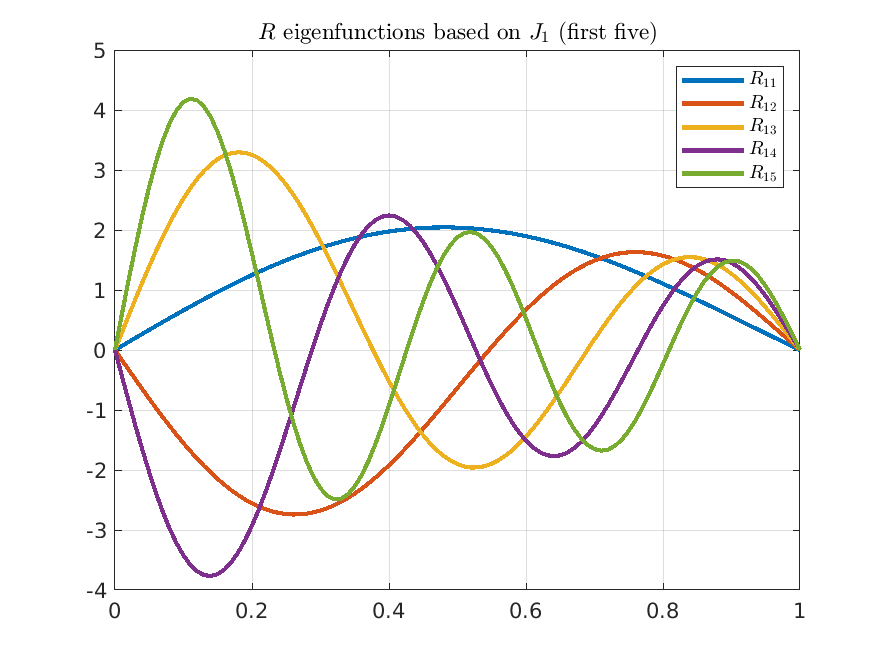
where \(z_{kn}\) is the \(n\)-th zero of the Bessel function of order \(k\), \(\Theta _k\) is as in (12.2) and (to make the eigenvectors orthonormal in \(L^2(0,b;r)\))
\[ R_{kn}(r)=\frac {\sqrt {2}}{bJ_{k+1}(z_{kn})}~J_k\left (\frac {z_{k n}}{b}r\right ). \]
The solution of the heat equation on the disc
\(\seteqnumber{0}{12.}{2}\)\begin{gather*} \partial _t u=\partial _{xx} u+\partial _{yy} u,\qquad t>0,~x^2+y^2<b^2,\\ u(t,x,y)=0,\qquad t>0,~x^2+y^2=b^2,\\ u(0,x,y)=u^0(x,y),\qquad ~x^2+y^2<b^2, \end{gather*} then is (using Cartesian coordinates on the left and polar coordinates on the right)
\[ u(t,x,y)=\sum _{n=1}^\infty \e ^{\lambda _{0n}t} \frac {1}{\sqrt {2\pi }}A_{0n}R_{0n}(r)+ \sum _{n=1}^\infty \sum _{k=1}^\infty \e ^{\lambda _{kn}t} \left (A_{kn}\frac {1}{\sqrt {\pi }}\cos (k\theta )R_{kn}(r) +B_{kn}\frac {1}{\sqrt {\pi }}\sin (k\theta )R_{kn}(r)\right ), \]
where (using a mixture of Cartesian and polar coordinates in the notation)
\(\seteqnumber{0}{12.}{2}\)\begin{gather*} A_{0n}=\int _{B_b(0)} u^0(x,y)\frac {1}{\sqrt {2\pi }}R_{0n}(r)\,dxdy,\\ A_{kn}=\int _{B_b(0)} u^0(x,y)\frac {1}{\sqrt {\pi }}\cos (k\theta )R_{kn}(r)\,dxdy,\\ B_{kn}=\int _{B_b(0)} u^0(x,y)\frac {1}{\sqrt {\pi }}\sin (k\theta )R_{kn}(r)\,dxdy, \end{gather*} which purely in polar coordinates is
\(\seteqnumber{0}{12.}{2}\)\begin{gather*} A_{0n}=\int _0^{2\pi }\int _0^b u^0(r\cos (\theta ),r\sin (\theta ))\frac {1}{\sqrt {2\pi }}R_{0n}(r)\,rdrd\theta ,\\ A_{kn}=\int _0^{2\pi }\int _0^b u^0(r\cos (\theta ),r\sin (\theta ))\frac {1}{\sqrt {\pi }}\cos (k\theta )R_{kn}(r)\,rdrd\theta ,\\ B_{kn}=\int _0^{2\pi }\int _0^b u^0(r\cos (\theta ),r\sin (\theta ))\frac {1}{\sqrt {\pi }}\sin (k\theta )R_{kn}(r)\,rdrd\theta . \end{gather*}