Chapter 11 Frobenius’ method

Let \(\sigma \geq 0\). We consider Bessel’s equation of order \(\sigma \) (note the the historical term order for the parameter \(\sigma \) is unfortunate since it clashes with the notion of order of a differential equation)

\begin{equation} \label {eq:Bessel} x^2u''+xu'+(x^2-\sigma ^2)u=0. \end{equation}

We make the Ansatz

\[ u(x)=x^\sigma \sum _{k=0}^\infty a_kx^k=\sum _{k=0}^\infty a_kx^{k+\sigma }. \]

We differentiate this term-by-term to obtain

\[ u'(x)=\sum _{k=0}^\infty (k+\sigma )a_kx^{k+\sigma -1},\qquad u''(x)=\sum _{k=0}^\infty (k+\sigma )(k+\sigma -1)a_kx^{k+\sigma -2}. \]

Substituting this into (11.1) gives

\[ x^2\sum _{k=0}^\infty (k+\sigma )(k+\sigma -1)a_kx^{k+\sigma -2} +x\sum _{k=0}^\infty (k+\sigma )a_kx^{k+\sigma -1} +(x^2-\sigma ^2)\sum _{k=0}^\infty a_kx^{k+\sigma }=0, \]

which we re-write as

\[ \sum _{k=0}^\infty (k+\sigma )(k+\sigma -1)a_kx^{k+\sigma } +\sum _{k=0}^\infty (k+\sigma )a_kx^{k+\sigma } +\sum _{k=0}^\infty a_kx^{k+\sigma +2} -\sum _{k=0}^\infty \sigma ^2a_kx^{k+\sigma }=0. \]

We shift the index in the third term by defining \(n:=k+2\) (so that \(k=n-2\)) to obtain for this third term

\[ \sum _{k=0}^\infty a_kx^{k+\sigma +2}=\sum _{n=2}^\infty a_{n-2}x^{n+\sigma }. \]

We then obtain (after simplification)

\[ \sum _{k=0}^\infty k(k+2\sigma )a_kx^{k+\sigma } +\sum _{k=2}^\infty a_{k-2}x^{k+\sigma }=0. \]

We can now factor out \(x^\sigma \) and obtain

\[ \sum _{k=0}^\infty k(k+2\sigma )a_kx^{k} +\sum _{k=2}^\infty a_{k-2}x^{k}=0. \]

We can write this as

\[ \sum _{k=0}^\infty b_k x^k=0,\qquad b_k=\begin {cases} k(k+2\sigma )a_k&k\in \{0,1\}\\ k(k+2\sigma )a_k+a_{k-2}&k\geq 2. \end {cases} \]

We must then have that \(b_k=0\) for all \(k\). For \(k=0\) this gives \(0=0\), for \(k=1\) this gives \((1+2\sigma )a_1=0\), which gives \(a_1=0\). For \(k\geq 2\) we have the following relation between the coefficients

\[ k(k+2\sigma )a_k+a_{k-2}=0, \]

which gives

\[ a_k=\frac {-1}{k(k+2\sigma )}a_{k-2},\qquad k\geq 2. \]

Since \(a_1=0\) we obtain that \(a_{2k+1}=0\) for all \(k\) and we have that \(a_0\) uniquely determines \(a_{2k}\) for all \(k\). We then obtain

\[ u(x)=a_0\sum _{k=0}^\infty \frac {(-1)^k}{2^{2k}k!(1+\sigma )(2+\sigma )\cdots (k+\sigma )}x^{2k+\sigma }. \]

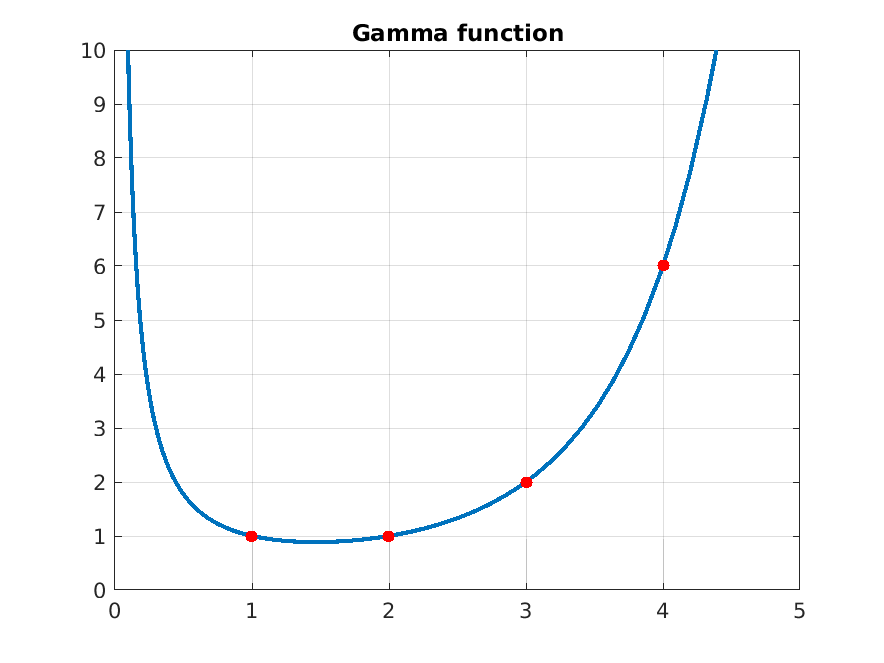
  • Remark. We recall the Gamma function (the continuous extension of the factorial), defined for \(z>0\) by

    \[ \Gamma (z)=\int _0^\infty t^{z-1}\e ^{-t}\,dt, \]

    which satisfies \(\Gamma (z+1)=z\Gamma (z)\) and \(\Gamma (n+1)=n!\) when \(n\in \mN _0\).

    (image)

In terms of the Gamma function we can write the solution with the (convenient) choice \(a_0=\frac {1}{2^\sigma \Gamma (\sigma +1)}\) as

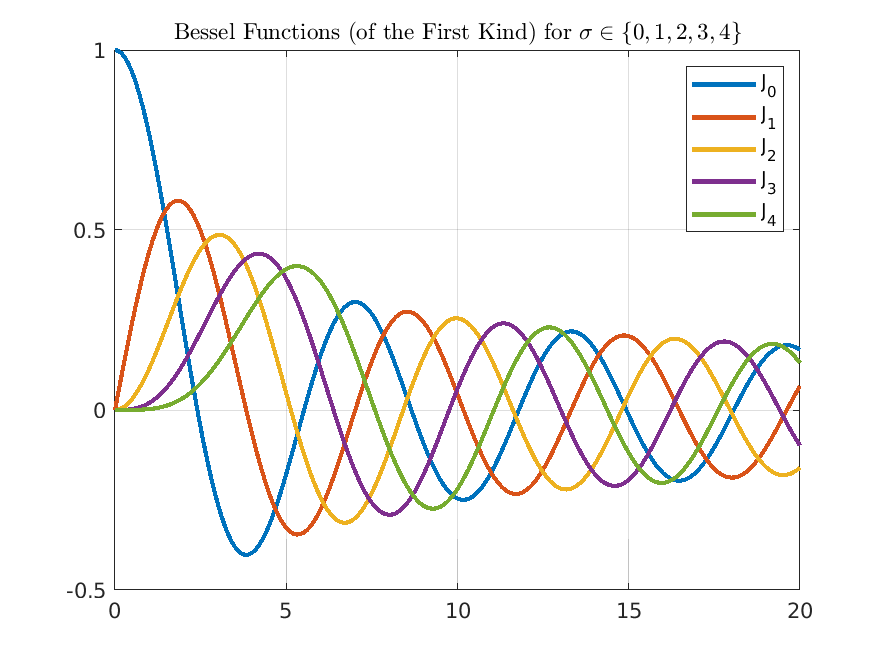
\[ J_\sigma (x):=\sum _{k=0}^\infty \frac {(-1)^k}{k!\Gamma (k+\sigma +1)}\left (\frac {x}{2}\right )^{2k+\sigma }, \]

which is called the Bessel function of order \(\sigma \) of the first kind.

In the special case where \(\sigma \) is an integer we obtain

\[ J_\sigma (x):=\sum _{k=0}^\infty \frac {(-1)^k}{k!(k+\sigma )!}\left (\frac {x}{2}\right )^{2k+\sigma }. \]

(image)
(image)