3 Trees and bipartite graphs

3.1 Trees

An acyclic graph is one that contains no cycles. A tree is a connected acyclic graph. A leaf is a vertex of degree 1.

Proposition 3.1 Trees are minimally connected, that is, $G=(V,E)$ is a tree if and only if it is connected but \[G-e = (V,E \setminus \{e\})\] is not for all $e \in E$.

Proof. ($\Leftarrow$) Suppose $G$ is connected, but is not a tree, then it contains a cycle $C=e_1 \ldots e_n$. If $e_1=uv$ then $P=e_2 \ldots e_n$ is apath from $v$ to $u$ in $G-e_1$. Thus $G-e_1$ is connected.

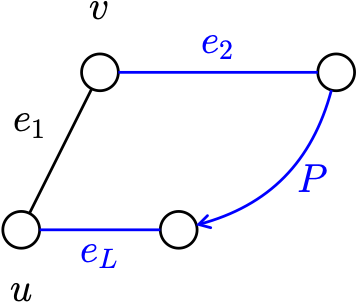
($\Rightarrow$) Suppose $G$ is a tree, containing an edge $e=uv$. $P=e$ is a path from $u$ to $v$ in $G$.

There is no other such path; because if there was one, say $Q$, then $QP$ would be a cycle.

Therefore, $u$ and $v$ are not connected in $G-e$. The same arguments hold for all $e \in E$.

Proposition 3.2 Trees are maximally acyclic, that is, $G$ is a tree if and only if it is acyclic but \[G + e = (V,E \cup \{e\})\] is not, for any $e=uv \not\in E$, $u,v \in V$.

Proof. ($\Rightarrow$) Suppose $G=(V,E)$ is a tree and $e=uv \not\in E$. Since $G$ is connected, there exists a path $P:u \to v$ in $G$ that does not use $e$. Thus $Pe$ is a cycle in $G+e$.

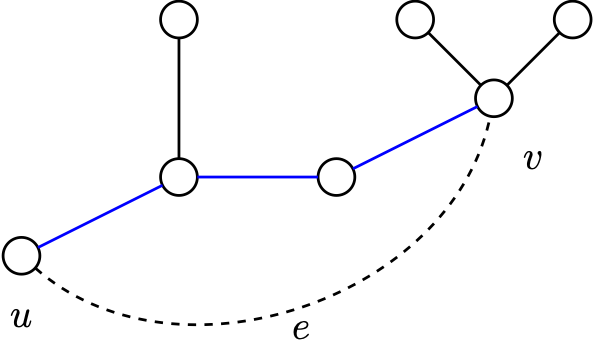
($\Leftarrow$) Acyclic graphs are either trees (connected) or forests (disconnected). If $u$ and $v$ are not connected in $G$, then $e=uv$ is the only $u \to v$ path in $G+e$, so $G+e$ is also acyclic.

Therefore a maximally acyclic graph must be connected – i.e., it must be a tree.

Proposition 3.3 The following are equivalent:

$G$ is a tree.
Any two vertices in $G$ are connected by a unique path.
$G$ is acyclic and $|E| = |V| - 1$.

Proof. Exercise

Proposition 3.4 Trees have leaves. Specifically, every tree $G$ has at least $\Delta(G)$ leaves.

Proof. For any graph $G=(V,E)$, write $\ell$ for the number of leaves. From the Handshaking lemma: \[\begin{aligned} 2 |E| &= \sum_{v \in V} d(v) \\ &= \ell + \sum_{v \in V, d(v) \geq 2} d(v)\\ &\geq \ell + \Delta(G) + 2 (|V| - \ell -1) \end{aligned}\]

Now, if $\ell < \Delta(G)$, then \[2|E| > 2 \ell + 2 (|V| - \ell -1),\] so $|E| > |V| - 1$ and $G$ is not a tree by Theorem 3.3.

Spanning Trees

We say $G' \subseteq G$ spans $G$ if $V' = V$. A spanning tree of a graph $G$ is a subgraph that

spans $G$, and
is a tree.

Proposition 3.5 Every connected graph has a spanning tree.

Proof. A finite graph $G$ has finitely many subgraphs, so it is possible to find a tree $T \subseteq G$ such that $T$ has at least as many vertices as any other tree subgraph of $G$.

We will prove $T$ spans $G$. Seeking contradiction, suppose $\exists v \in V$ not included in $T$. Since $G$ is connected, $\exists P : u \to v$ a path from a vertex $u \in T$ to $v$.

Write $w$ for the last vertex of $T$ that appears in $P$, so that $P=QR$ where $Q : u \to w$ and $R : w \to v$ are paths in $G$.

But then $T \cup R$ is a tree subgraph of $G$ that is strictly larger than $T$. Contradiction.

“Spanning Tree Protocol” (STP)

Problem: How to design computer networks that can route information quickly but are robust to failures of components.

Solution: Connect network segments with “bridges” that organise themselves into a spanning tree. Messages are routed via the tree, and if a bridge fails, we find a new tree.

Proposition 3.6 (Kirchhoff’s matrix tree theorem) Let $A$ be the adjacency matrix, and $D$ the diagonal matrix of degrees of a connected graph $G$ on $n$ vertices.

The matrix $L=D-A$ has eigenvalues \[\mu_1 \geq \ldots \geq \mu_{n-1} > \mu_n = 0,\] and \[(\text{number of spanning trees of $G$}) = \dfrac{1}{n} \prod_{i=1}^{n-1} \mu_i\]

Proof. Too long!

Caley’s formula states that the complete graph on $n$ vertices has $n^{n-2}$ spanning trees.

To see this, we note that the eigenvalue equation \[\mu v_j = [(D-A)\boldsymbol{v}]_j=(n-1)v_j-\sum_{k\neq j}v_k = nv_j-\sum_{k}v_k\] is satisfied with $\mu=0$, $v_j\equiv 1$ or with $\mu=n$ by vectors with entries summing to zero (this space has dimension $n-1$).

So Kirchhoff says the number of spanning trees is \[\dfrac{1}{n} \prod_{i=1}^{n-1} \mu_i= \dfrac{1}{n} \prod_{i=1}^{n-1} n = n^{n-2}\,.\]

3.2 Bipartite graphs

A graph $G=(V,E)$ is bipartite if $V$ can be written as a disjoint union $V=X \cup Y$, $X \cap Y = \emptyset$, such that each edge in $E$ is of the form $e=xy$ where $x \in X$ and $y \in Y$.

The complete bipartite graph $K_{n,m}$ has $|X|=n$, $|Y|=m$ and has every possible edge. Note $K_{n,m} \simeq K_{m,n}$.

$K_{2,3}$:

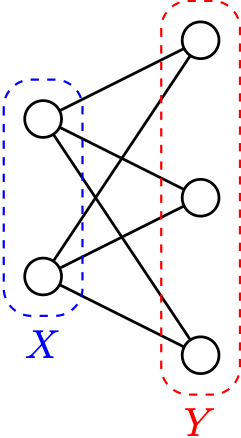
Proposition 3.7 Trees are bipartite.

Proof. Let $G=(V,E)$ be a tree and pick any vertex $u \in V$ to be the “root.” Write $P_{uv}$ for the unique path in $G$ from $u$ to $v$, for any other vertex $v \in V$. We choose \[\begin{aligned} && X = \{v : \text{$|P_{uv}|$ is even}\}\\ && Y = \{v : \text{$|P_{uv}|$ is odd}\}\end{aligned}\]

Now, for each $v \in V$, $P_{uv}$ is either odd or even but not both, so \[X \cup Y = V \quad \text{and} \quad X \cap Y = \emptyset.\]

Suppose $e=ab \in E$ is an edge. Note that $P_{au}^{-1} P_{ub}$ is a walk from $a$ to $b$, which contains a path. By uniqueness, this path is $e$.

Without loss of generality, assume $e \in P_{ua}$, so $P_{ub}e$ is a path of length $|P_{ub}|+1$ from the root $u$ to $a$.

Thus $|P_{ua}|$ and $|P_{ub}|$ have opposite parity and $a$ and $b$ are in different parts.

Proposition 3.8 A graph is bipartite if and only if it contains no cycles of odd length.

Proof. It is enough to consider connected graphs since both properties apply to all connected components.

($\Rightarrow$) Suppose $G$ is bipartite with parts $X$ and $Y$. Let $P$ be a path starting in $X$. The vertices of $P$ belong alternately to $X$ then $Y$, so if $P$ has odd length, then the final vertex is in $Y$ and $P$ is not a cycle.

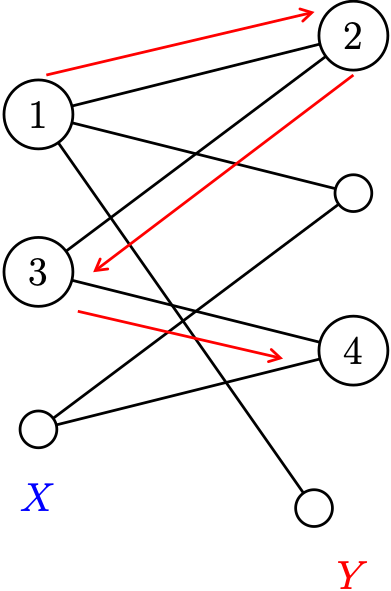
($\Leftarrow$) Suppose $G$ is a connected graph without odd cycles. Let $T \subset G$ be a spanning tree. $T$ is bipartite, call the parts $X$ and $Y$, so that \[X \cup Y = V\quad \text{and}\quad X \cap Y = \emptyset.\]

We have to check that no edges join vertices of $X$ to other vertices of $X$, and the same for $Y$.

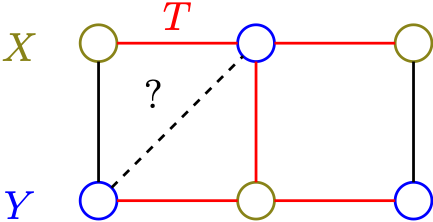
Suppose (without loss of generality) $u,v \in X$. There is a unique path $P: v \to u$ in $T$ and it has even length because $T$ is bipartite and $u$ and $v$ are in the same part.

Thus, $e=uv$ cannot be an edge in $G$ because then $Pe$ would be an odd length cycle. Therefore, all sdges of $G$ have one endpoint in $X$ and one in $Y$, so $G$ is bipartite.

The toroidal lattice: $G=$

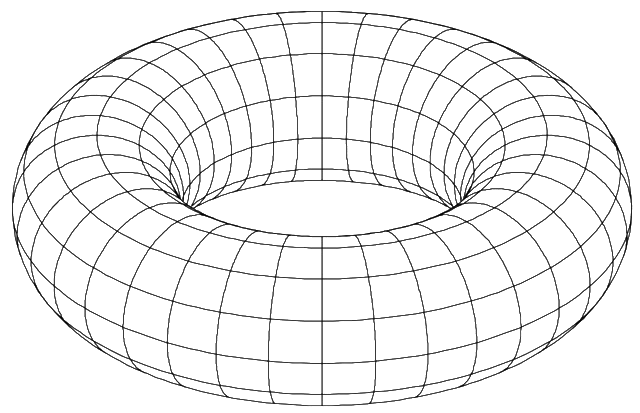
Vertex set is $V=\{1,\dots,n\}^2$, edges are defined by the rule $(a,b)\sim(c,d)$ if $a=c$ and $|b-d|=1\mod n$ or $b=d$ and $|a-c|=1\mod n$.

If $n$ is even then $G$ contains no odd cycles. To see this, note that any walk starting and ending at the same vertex must take an even number of horizontal steps and an even number of vertical steps.

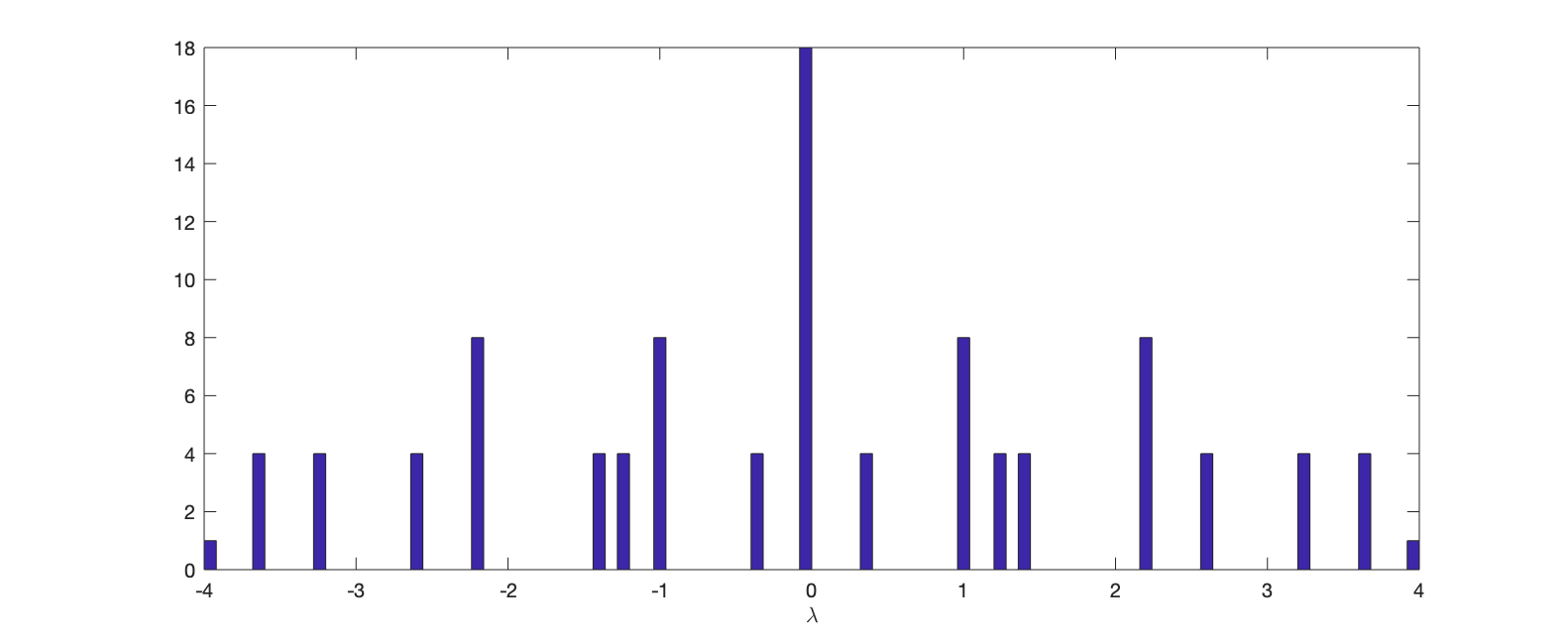
If $C_n$ is the adjacency of a cycle of length $n$, then the adjacency matrix of the graph of the toroidal lattice can be written $A_n=C_n\otimes I_n+I_n\otimes C_n$. Here is a histogram of the eigenvalues of $A_{10}$:

Proposition 3.9 A graph is bipartite if and only if the spectrum of its adjacency matrix is symmetric about zero.

Proof. ($\Rightarrow$) Let $G$ be bipartite with parts $X$ and $Y$. Label the vertices $1$ to $n=|V|$, so that the vertices in $X$ come first. The adjacency matrix has the form \[A = \begin{pmatrix} 0 & B \\ B^T & 0 \end{pmatrix}\] where $B$ is an $|X| \times |Y|$ matrix.

Suppose $\lambda \in \mathrm{spec}(A)$, that is \[\exists \boldsymbol{v} \in \mathbb{R}^n \quad \text{s.t.} \quad A \boldsymbol{v} = \lambda \boldsymbol{v}.\]

Write \[\boldsymbol{v} = \begin{pmatrix} \boldsymbol{x} \\ \boldsymbol{y} \end{pmatrix} \quad \text{for $\boldsymbol{x} \in \mathbb{R}^{|X|}$, $\boldsymbol{y} \in \mathbb{R}^{|Y|}$},\] so that \[\begin{aligned} A \boldsymbol{v} = \lambda \boldsymbol{v} &\Leftrightarrow \begin{pmatrix} 0 & B \\ B^T & 0 \end{pmatrix} \begin{pmatrix} \boldsymbol{x} \\ \boldsymbol{y} \end{pmatrix} = \lambda \begin{pmatrix} \boldsymbol{x} \\ \boldsymbol{y} \end{pmatrix} \\ &\Leftrightarrow B \boldsymbol{y} = \lambda \boldsymbol{x} \quad \text{and}\quad B^T \boldsymbol{x} = \lambda \boldsymbol{y}.\end{aligned}\]

Now, let \[\boldsymbol{w} = \begin{pmatrix} \boldsymbol{x} \\ - \boldsymbol{y} \end{pmatrix}\]

\[\begin{aligned} A \boldsymbol{w} &= \begin{pmatrix} 0 & B \\ B^T & 0 \end{pmatrix} \begin{pmatrix} \boldsymbol{x} \\ - \boldsymbol{y} \end{pmatrix}= \begin{pmatrix} - B \boldsymbol{y} \\ B^T \boldsymbol{x} \end{pmatrix}\\ &= \begin{pmatrix} - \lambda \boldsymbol{x} \\ \lambda \boldsymbol{y} \end{pmatrix} = - \lambda \boldsymbol{w},\end{aligned}\] so $-\lambda \in \mathrm{spec}(A)$ also.

($\Leftarrow$) Let $G$ be a graph with adjacency matrix $A$ such that $\mathrm{spec}(A)$ is symmetric about zero. In particular, $\lambda_1=-\lambda_n$, where $\lambda_1$ is the “Frobenius” eigenvalue with largest magnitude and \[\lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_n.\]

Write $\boldsymbol{v}$ for a unit length, i.e. \[\boldsymbol{v}^T \boldsymbol{v} = \sum_{i} v_i^2 = 1,\] eigenvector corresponding to $\lambda_n$.

So \[A \boldsymbol{v} = \lambda_n \boldsymbol{v} = -\lambda \boldsymbol{v}.\]

Write $\boldsymbol{u}$ for the vector with entries $u_i = |v_i|$.

By Theorem 1.8 (ii) \[\boldsymbol{w}^T A \boldsymbol{w} \leq \lambda_1 \sum_i w_i^2 \quad \forall \boldsymbol{w} \in \mathbb{R}^n.\]

Applied to our case \[\begin{aligned} \lambda_1 &= - \lambda_n \boldsymbol{v}^T \boldsymbol{v}\\ &= -\boldsymbol{v}^T A \boldsymbol{v} \\ &= - \sum_{i,j} A_{ij} v_i v_j \\ &\leq \sum_{i,j} A_{ij} |v_i| |v_j| \\ &= \boldsymbol{u}^T A \boldsymbol{u} \\ &\leq \lambda_1 \sum_i u_i^2 \\ &= \lambda_1.\end{aligned}\]

So in fact we must have \[- \sum_{i,j} A_{ij} v_i v_j = \sum_{i,j} A_{ij} |v_i| |v_j|.\]

Since every term on the RHS is positive we require a matching negative from every term on the LHS.

Thus, $v_i v_j < 0$ when $i \sim j$.

Write $X = \{ i : v_i > 0 \}$ and $Y = \{ i : v_i < 0 \}$, then $A_{ij}=0$ if $i,j \in X$ or $i,j \in Y$. So $G$ is bipartite with parts $X$ and $Y$.