6 Drawing
6.1 Crossings
A plane drawing of a graph is a pair \((V,E)\) such that:
vertices \(v \in V\) are points in \(\mathbb{R}^2\)
edges \(e \in E\) are continuous curves \(e:[0,1] \to \mathbb{R}^2\)
edge endpoints are vertices, i.e. \(e(0), e(1) \in V\)
the interior of an edge contains no vertices
the pair \(G=(V, \sigma (E))\) is a simple graph, where \(\sigma(e) = \{e(0), e(1)\}.\)
The crossing number of a plane drawing is the number of pairs of edges that share interior points.
The crossing number \(\mathrm{cr}(G)\) of a graph \(G\) is the smallest crossing number possible in a plane drawing of \(G\).
Mathematician Paul Turán wrote in his welcome note in the first edition of the Journal of Graph theory
“In July 1944 the danger of deportation was real in Budapest, and a reality outside Budapest. We worked near Budapest, in a brick factory. There were some kilns where the bricks were made and some open storage yards where the bricks were stored. All the kilns were connected by rail with all the storage yards. The bricks were carried on small wheeled trucks to the storage yeards. All we had to do was to put the bricks on the trucks at the kilns, push the trucks to the storage yards, and unload them there. We had a reasonable piece rate for the trucks, and the work itself was not difficult; the trouble was only at the crossings. The trucks generally jumped the rails there, and the bricks fell out of them; in short this caused a lot of trouble and loss of time which was rather precious to all of us (for reasons not to be discussed here).”
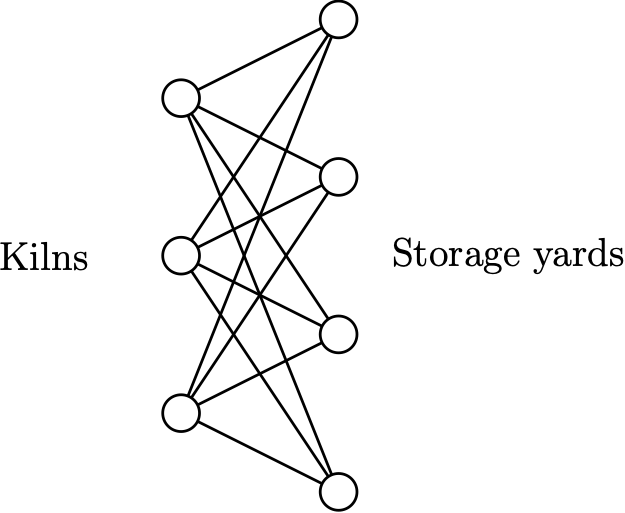
This raises the problem of how to arrange a graph in the plane with the minimum number of crossings.
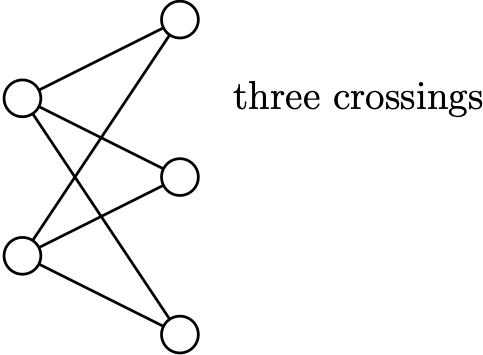

Conjecture: \[\mathrm{cr}(K_{n,m}) = \lfloor\dfrac{m}{2}\rfloor \lfloor\dfrac{m-1}{2}\rfloor \lfloor\dfrac{n}{2}\rfloor \lfloor\dfrac{n-1}{2}\rfloor\]
Proof. Coming later on…
6.2 Plane graphs
If \(\mathrm{cr}(G)=0\), then we say \(G\) is planar (that is, it can be drawn in the plane with no crossings). A plane drawing with no crossings is called a plane graph.
A plane graph \(G\) divides \(\mathbb{R}^2\) into a number of disjoint connected regions called faces. Exactly one face is unbounded, this is the outer face or \(F_0\).
The bounded faces are called interior faces, write \(\partial F_i\) for the boundary of \(F_i\).

Some general facts about faces
The outer face is unique (i.e. it is the only unbounded face).
Each edge belongs to the boundary of at least one and at most two faces.
Each cycle surrounds at least one interior face.
The boundary of each interior face contains exactly one cycle.
Proof. Proof of Euler’s formula. Induction on \(|F|\). If \(|F|=1\), then \(G\) contains no cycle since it would surround an interior face. So \(G\) is connected and acyclic, hence it is a tree and \(|E| = |V| -1\). So the claim holds.
Now suppose \(|F| > 1\) and the claim holds for graphs with fewer faces. Since \(|F|>1\) we can choose an edge \(e\) that is not a bridge and hence lies on the boundary of two faces.
The graph \(H=G-e\) is connected and plane, but has one fewer faces.

\[\begin{aligned} |F_H| &= |F| - 1\\ |V_H| &= |V|\\ |E_H| &= |E| - 1.\end{aligned}\]
By the induction hypothesis \[\begin{aligned} |V_H| - |E_H| + |F_H| &= 2\\ \Rightarrow\quad |V| - (|E|-1) + (|F|-1) &= 2\\ \Rightarrow\quad |V| - |E| + |F| &= 2.\end{aligned}\]
Proof. Consider a drawing of \(G\) with \(c=\mathrm{cr}(G)\) crossings. Place an additional vertex on each crossing
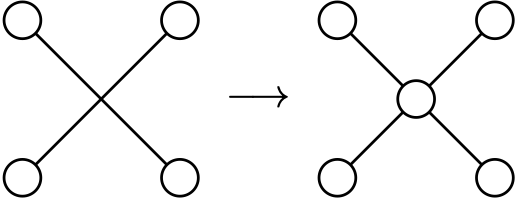
to obtain a plane graph \(G^{\prime}=(V^{\prime},E^{\prime})\) with \[|V^{\prime}| = |V| + c \quad \text{and}\quad |E^{\prime}| = |E| + 2c.\]
Every edge in \(G^{\prime}\) lies on the boundary of at most two faces, and every face is bounded by at least \(3\) edges, so \[2|E^{\prime}| \geq 3|F^{\prime}|.\]
Thus, by Euler’s formula \[\begin{aligned} 6 &= 3 (|V^{\prime}| - |E^{\prime}| + |F^{\prime}|) \\ &\leq 3|V^{\prime}| - |E^{\prime}|\\ &= 3 |V| + 3c - |E| - 2c\\ \Rightarrow \quad c &\geq |E| - 3|V| + 6\end{aligned}\]
Proof. Proof of Theorem 6.1. The claim is that \[\mathrm{cr}(G) \geq \dfrac{4|E|^3}{243 |V|^2}.\]
We use a random graph argument. Consider a drawing of \(G\) with \(\mathrm{cr}(G)\) crossings. Create a random subgraph \[G^{\prime} = (V^{\prime}, E^{\prime}] \subseteq G\] by independently deleting each vertex with probability \(1-p\).
Each vertex has a chance \(p\) to be included in \(G^{\prime}\), so \[\mathbb{E}|V^{\prime}| = p |V|.\]
For an edge to appear in \(G^{\prime}\) we need both endpoints to be included, so \[\mathbb{E}|E^{\prime}| = p^2 |E|.\]
Finally, each crossing involves four vertices, so \[\mathbb{E} \mathrm{cr}(G^{\prime}) = p^4 \mathrm{cr}(G).\]
Applying Lemma 6.3 to \(G^{\prime}\), we have \[\mathrm{cr}(G^{\prime}) \geq |E^{\prime}| - 3 |V^{\prime}|.\]
This holds for all \(p \in [0,1]\), so what is the best we can do?
\[\begin{aligned} & \mathrm{cr}(G) \geq f(p) := \dfrac{|E|}{p^2} - \dfrac{3|V|}{p^3}\\ & f^\prime(p) = -\dfrac{2|E|}{p^3} + \dfrac{9|V|}{p^4} = 0\\ &\Rightarrow p^* = \dfrac{9|V|}{2|E|},\end{aligned}\] so \[\begin{aligned} \mathrm{cr}(G) &\geq f_{\max} = f \left(\dfrac{9|V|}{2|E|}\right)\\ & = \dfrac{4|E|^3}{81 |V|^2} - \dfrac{24|E|^3}{729|V|^2}\\ & = \left( \dfrac{36-24}{729} \right) \dfrac{|E|^3}{|V|^2} = \dfrac{4}{243} \dfrac{|E|^3}{|V|^2}. \end{aligned}\]
A platonic solid is a regular convex polyhedron with congruent faces of regular polygons. In graph theory terms, a platonic solid is a plane graph in which every vertex has degree \(q>2\) and every face is bounded by a \(p\)-cycle, for \(p,q\in\mathbb{N}\)
Cube:


Proof. Let \(G\) be a plane graph of a platonic solid. Every vertex has degree \(q\), so \[2 |E| = q |V|\] also, every face is bounded by a \(p\)-cycle, so \[2 |E| = p |F|.\]
Then Euler’s formula gives \[\begin{aligned} && \dfrac{2|E|}{q} - |E| + \dfrac{2 |E|}{p} = 2 \\ &\Rightarrow& \dfrac{1}{p} + \dfrac{1}{q} = \dfrac{1}{|E|} + \dfrac{1}{2} > \dfrac{1}{2}\end{aligned}\] since \(|E|>0\).
We know \(p>2\) and \(q>2\), so the only possibilities are:
\(p=3\), \(q=3\) Tetrahedron
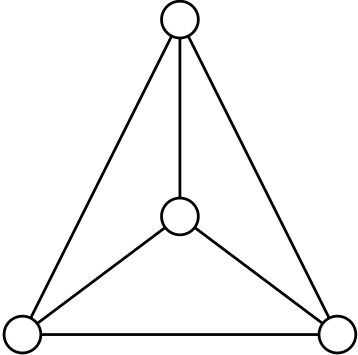
\(p=4\), \(q=3\) Cube

\(p=5\), \(q=3\) Dodecahedron

\(p=3\), \(q=4\) Octahedron

\(p=3\), \(q=5\) Icosahedron
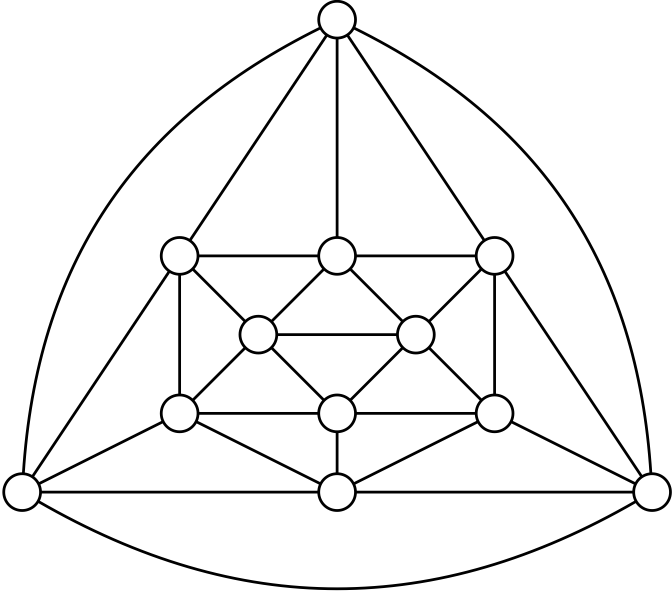
Kuratowski’s theorem
A subdivision of a graph \(G\) is another graph \(G^{\prime}\) in which some edges of \(G\) have been replaced by paths of length \(>1\).
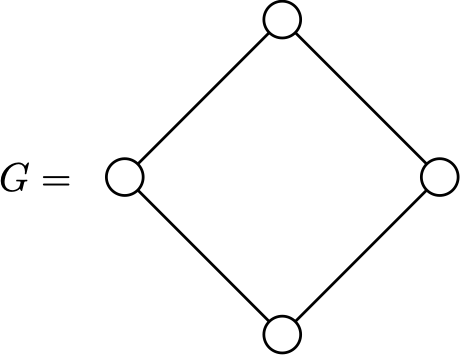
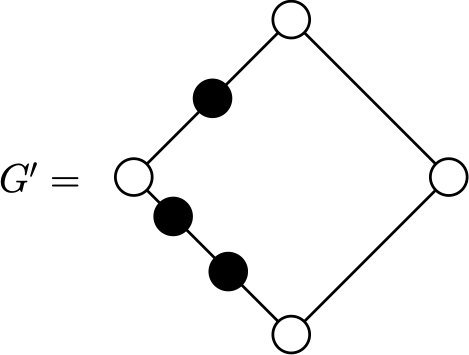
Proof. (\(\Rightarrow\)) Suppose \(H \subseteq G\) is a subdivision of either \(K_5\) or \(K_{3,3}\).
Deleting the additional vertices from a drawing of \(H\) gives a drawing of \(K_5\) or \(K_{3,3}\), which we know must have a crossing (see problem sheet). So \(G\) must have a crossing too.
(\(\Leftarrow\)) Too long!
A plane graph is a plane triangulation if the boundary of each of its faces (including the outer face) is a triangle.
An icosahedron:

Proof. It is sufficient to consider only plane triangulations since any plane graph is a subgraph of a plane triangulation (add edges until every face is bounded by a triangle).
We will prove by induction that for any face \(F_i\) in a plane triangulation \(G\), there exists a plane drawing of \(G\) with straight edges and \(F_i\) as the outer face.
Base case: If \(|V| = 3\), then \(G\) is a triangle, so the following will do:

Now assume the claim holds for all graphs with fewer than \(|V|\) vertices, and let \(F_i\) be a triangular face with \[\partial F_i = \{uv, vw, wu\}.\]
Since every face is a triangle, we have \(2|E| = 3|F|\), so by Euler’s formula (\(|V|-|E|+|F|=2\)) we have \[\sum_{x \in V} d(x) = 2|E| = 6|V| - 12.\]
Since \(|V| > 3\), \(\delta(G)\geq 3\), so there must exist at least four vertices with degree less than \(6\). Choose any \(x \neq u, v, w\) with \(d(x)<6\). Find a new graph \(G^{\prime}\) by deleting \(x\) and triangulating the newly formed face.
By induction, \(G^{\prime}\) has a straight line drawing with \(uvw\) as the outer face. Put back \(x\) and join with straight edges to its original neighbours.

6.3 Colouring drawings
Hard!
Proof. We will use Theorem 5.7, \[\chi(G) \leq 1 + \max_{H \subseteq G} \delta(H).\]
Let \(H \subseteq G\). If \(H\) is acyclic, then its connected components are trees (which have leaves), so \(\delta(H)\leq 1\).
Otherwise, \(g(H) \geq 4\) since \(G\) has no triangles.
Because \(H \subseteq G\), it must be planar, so from a question in the Problem Sheets, we have \[\begin{aligned} && \dfrac{|E_H|}{ |V_H| - 2} \leq \dfrac{g(H)}{g(H)-2} \leq 2\\ &\Rightarrow& \sum_{v \in H} d(v) = 2 |E_H| < 4 |V_H|. \end{aligned}\]
Therefore \(\delta(H) \leq 3\). \(H\) was arbitrary, so we conclude that \[\chi(G) \leq 1+ 3 = 4.\]
Art galleries
A polygon (or \(n\)-gon) is a planar region bounded by \(n\) straight edges. A point \(x\) in a polygon \(P\) sees a point \(y \in P\) if the straight line \(xy\) is contained in \(P\).
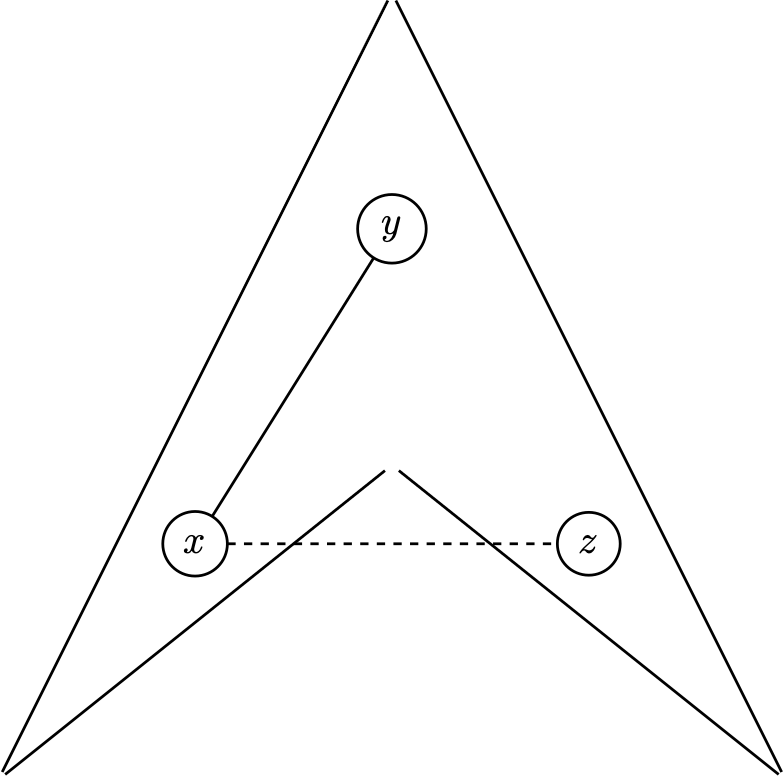
\(x\) sees \(y\) but not \(z\).
Proposition 6.10 To any \(n\)-gon \(P\) we may add edges to obtain a plane graph \(G\) such that:
the vertices of \(G\) are the corners of \(P\);
the boundary of the outer face of \(G\) is the boundary of the polygon;
every interior face of \(G\) is a triangle;
\(G\) contains a vertex of degree \(2\).
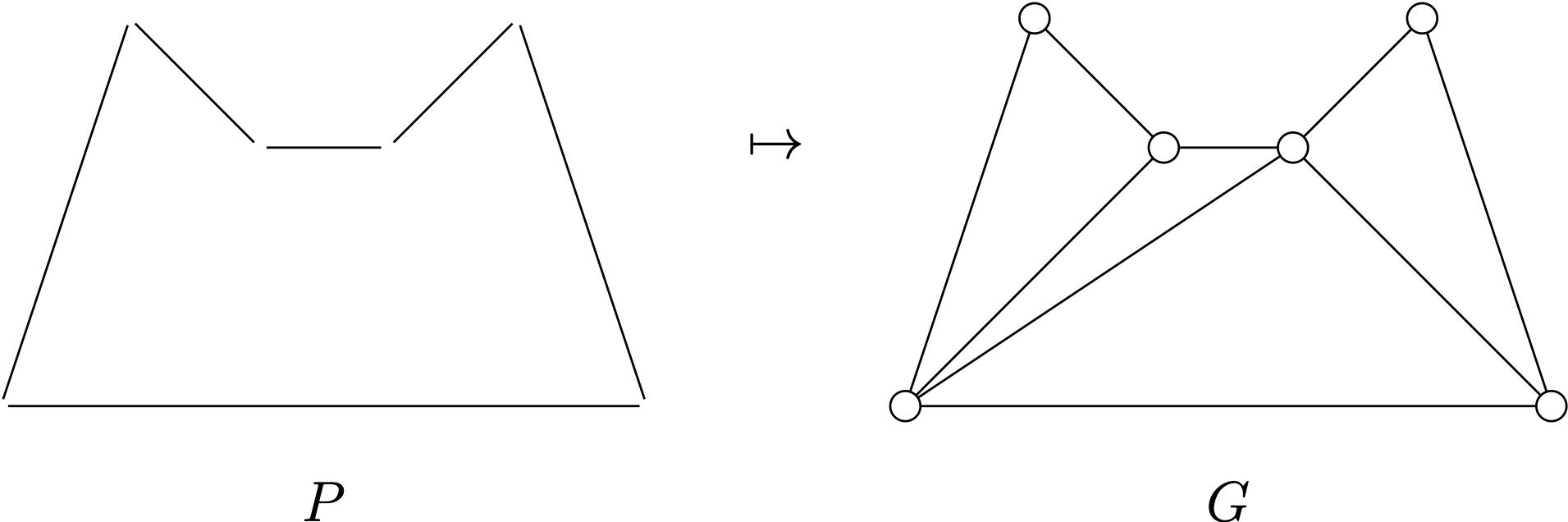
Proof. Parts i-iii use induction on \(n\)…
If \(n=3\) then \(P\) is already a triangle.
Let \(P\) be an \(n\)-gon and assume the claim holds for all smaller polygons. Pick any vertex \(v\) and call its neighbours \(u\) and \(w\).
If \(v\) can see another vertex \(x\), let \(L\) be the straight line \(vx\).
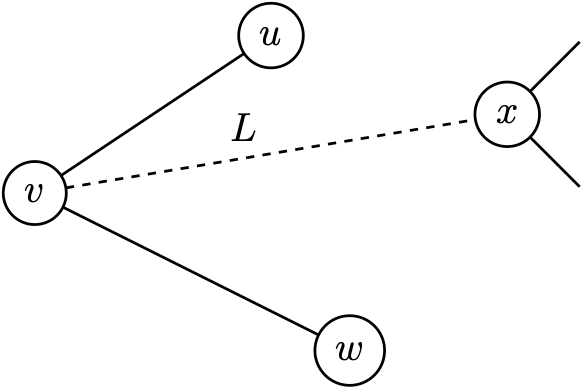
If \(v\) can only see \(u\) and \(w\), it follows that there are no other vertices in the triangle \(uvw\), so \(u\) and \(w\) can see each other.
Let \(L\) be the straight line \(uw\).
In either case, \(L\) divides \(P\) into two strictly smaller polygons.

Apply the induction hypothesis to divide these into triangles and join to find a triangulaton of \(P\).
For part iv, Consider the graph \(H\) formed by taking faces of \(G\) as vertices and joining them with an edge when they share part of a boundary, e.g.
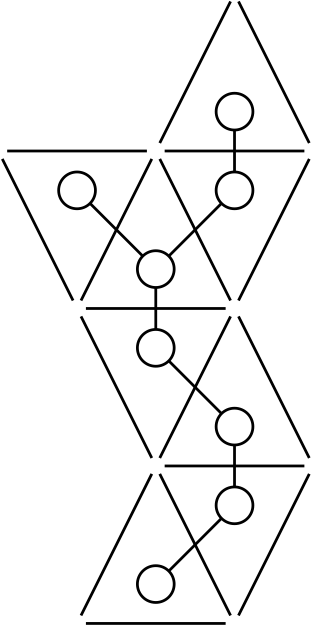
This graph \(H\) cannot contain a cycle, because it would surround a vertex of \(G\), but all vertices of \(G\) lie on the boundary of the outer face. Since \(H\) is a tree, it has leaves, these correspond to faces of \(G\) that share a boundary with only one other, and hence contain a vertex of degree \(2\).

Proof. Let \(P\) be a polygon and \(G\) a triangulation obtained in Proposition 6.10. Suppose every smaller such triangulation can be \(3\)-coloured. Find a vertex \(v\) of degree \(2\) in \(G\) and remove it.
Colour \(G-v\) with \(3\) colours, then extend to \(G\) by giving \(v\) the colour not used on its neighbours.
Proof. Proof of the Art Gallery Theorem 6.9. Let \(P\) be an \(n\)-gon. Triangulate it and \(3\)-colour the vertices. At least one colour is used no more than \(\dfrac{n}{3}\) times. Place guards on these vertices and between them they see every triangle and hence the whole of \(P\).