5 Colouring
5.1 Chromatic number
A \(k\)-colouring of a graph \(G=(V,E)\) is a map \(\beta: V \to \{1,\ldots,k\}\) such that \(\beta(u) \neq \beta(v)\) whenever \(uv \in E\). A graph \(G\) is \(k\)-colourable if there exists a \(k\)-colouring of \(G\).
The chromatic number \(\chi(G)\) is the smallest \(k\) such that \(G\) is \(k\)-colourable.
\(G=\)

\(3\)-colourable, but not \(2\)-colourable, so \(\chi(G)=3\).
Proof. (\(\Rightarrow\)) Suppose \(G\) is bipartite with parts \(X\) and \(Y\). Define \[\beta(v) = \begin{cases} 1 & \text{if $v \in X$}\\ 2 & \text{if $v \in Y$} \end{cases}\]
Then \[\begin{aligned} &uv \in E \quad \Rightarrow& \begin{cases} u\in X, v \in Y & \Rightarrow \beta(u)=1 \neq 2 = \beta(v)\\ u\in Y, v \in X & \Rightarrow \beta(u)=2 \neq 1 = \beta(v) \end{cases}\end{aligned}\]
(\(\Leftarrow\)) Suppose \(\chi(G)=2\) and let \(\beta\) be any \(2\)-colouring. Define \[\begin{aligned} & X = \beta^{-1} (1) := \{ v\in V : \beta(v)=1\}\\ & Y = \beta^{-1}(2)\end{aligned}\]
By definition of \(\beta\), each \(v\in V\) is in exactly one of \(X\) or \(Y\).
Finally, if \(uv \in E\), then \(\beta(u) \neq \beta(v)\), hence \(u\) and \(v\) are in different parts.
It’s tempting to think of short cycles as being responsible for a graph having a high chromatic number but…
Proof. Sketch. Draw a large graph at random.
Let \(\rho=N^{\frac{1}{2k}-1}\) and choose \(G_N\) to be an ERII random graph from \(G(N,\rho)\).
Write \(\alpha_N = \alpha(G_N)\) for the size of the largest subset of vertices in \(G_N\) that share no edges (called the independence number), and \(c_N\) for the number of cycles of length less than \(k\) in \(G_N\).
One can show that \[\begin{aligned} & \mathbb{P} \left(\alpha_N \geq \dfrac{N}{2k}\right) \to 0 \quad \text{as $N \to \infty$}\\ & \mathbb{P} \left(c_N \geq \dfrac{N}{2}\right) \to 0 \quad \text{as $N \to \infty$}. \end{aligned}\]
Let \(N\) be large enough that both probabilities are smaller than \(\dfrac{1}{2}\), then there must exist a graph \(H\) with fewer than \(\dfrac{N}{2}\) cycles of length less than \(k\) and \[\alpha(H) < \dfrac{N}{2k}.\]
From each short cycle in \(H\), delete one vertex. The graph obtained, \(G=(V,E)\) has \(g(G)\geq k\) and \(|V| \geq \dfrac{N}{2}\).
Moreover, \[\alpha(G) \leq \alpha(H) < \dfrac{N}{2k}\]
From problem sheet: \[\chi(G) \geq \dfrac{|V|}{\alpha(G)} > \dfrac{N/2}{N/2k} = k\]
5.2 Elementary bounds
Question: How can we estimate \(\chi(G)\) in terms of basic graph properties?
Proof. If a colouring uses the smallest possible number of colours, there must be edges between vertices of every possible pair of colours.
If \(\beta\) is a minimal colouring, then it uses \(\chi(G)\) colours. There are \(\binom{\chi(G)}{2}\) pairs of colours that must be joined by edges, so \[|E| \geq \dfrac{1}{2} \chi(G) (\chi(G)-1).\]

For fixed \(|E|\), \(\chi(G)\) must be sufficiently small. The boundary is found by solving \[\begin{aligned} & |E| = \dfrac{1}{2} \chi (\chi - 1)\\ &\Rightarrow & \chi^2 - \chi - 2 |E| = 0 \\ &\Rightarrow & \chi = \dfrac{1 \pm \sqrt{1+8|E|}}{2}\end{aligned}\]
Minus root is negative, therefore \[\chi(G) \leq \dfrac{1}{2} + \sqrt{\dfrac{1}{4} + 2|E|}.\]
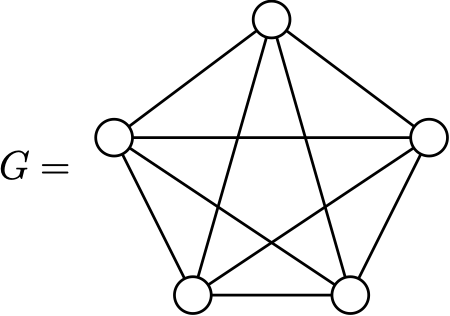
\[\begin{aligned} & |E| = 10 \\ & \chi(G) = 5 \leq \dfrac{1}{2} + \sqrt{\dfrac{1}{4} + 20} = 5\end{aligned}\]

\[\begin{aligned} & |E| = 10 \\ & \chi(G) = 2 \leq 5\end{aligned}\]
Can we do better?
Proof. We construct a colouring using a greedy algorithm: label the vertices \(v_1, \ldots, v_n\) and colour, so \[\beta(v_i) = \min \{ n \in \mathbb{N} : n \neq \beta(v_j) \text{ for $j < i$ with $v_j \sim v_i$} \}.\]
Since \(|\mathcal{N}(v_i)| \leq \Delta(G)\) we know that \[\beta(v_i) \leq \Delta(G) + 1.\]

\[\begin{aligned} & \Delta(G) = 2 \\ & \chi(G) = 3 \leq \Delta(G) + 1 = 3.\end{aligned}\]
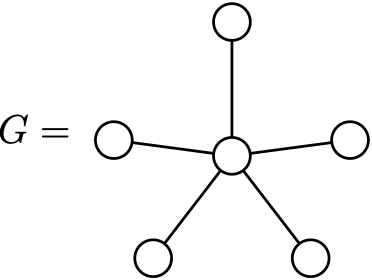
\[\begin{aligned} & \Delta(G) = 5 \\ & \chi(G) = 2 \leq \Delta(G) + 1 = 6.\end{aligned}\]
Proof. Suppose \(\chi(G)=k\) and \(|V|=n\), what is the maximum number of edges \(G\) may have? Write \[V_{c} = \{v : \beta(v) = c \} = \beta^{-1}(c)\] for a given \(k\)-colouring \(\beta\) and let \(n_c = |V_c|\).
If every possible edge is included, we have \[\begin{aligned} 2|E| &= \sum_{c=1}^k n_c \sum_{c^{\prime} \neq c} n_{c^{\prime}}\\ &= \sum_{c=1}^k n_c(n-n_c) \\ &= n^2 - \sum_{c=1}^k n_c^2.\end{aligned}\]
So the number of edges is maximised when \(\sum_{c=1}^k n_c^2\) is minimised, subject to the constraint that \(\sum_{c=1}^k n_c = n.\)
Solution by Largange multipliers.
Promote \(n_c\) to \(\mathbb{R}\) and look for minima of \[\Lambda = \underbrace{\sum_c n_c^2}_{\text{thing to minimise}} + \underbrace{\lambda}_{\text{Lagrange multiplier}} \underbrace{\left(\sum_c n_c - n\right)}_{\text{constraint}=0}\]
\[\begin{aligned} & \dfrac{\partial \Lambda}{\partial \lambda} = \sum_c n_c - n = 0\\ &\Rightarrow \text{contraint holds}\end{aligned}\]
\[\begin{aligned} & \dfrac{\partial \Lambda}{\partial n_c} = 2n_c + \lambda = 0\\ &\Rightarrow \text{all $n_c$ are equal}\\ &\Rightarrow n_c = \dfrac{n}{k}.\end{aligned}\]
Thus \[2|E| \leq n^2 - \sum_{c=1}^k \left(\dfrac{n}{k}\right)^2 = |V|^2 \left(1 - \dfrac{1}{k}\right)\]
\[\Rightarrow \quad \chi(G) \geq \dfrac{|V|^2}{|V|^2 - 2 |E|}.\]
5.3 Criticality
A \(k\)-colourable graph \(G\) is \(k\)-critical if \(\chi(G)=k\) and any strict subgraph \(H \subset G\) (i.e. \(H \neq G\)) is \((k-1)\)-colourable. In particular, \(G-e\) is \((k-1)\)-colourable for any edge \(e \in E\).

It is \(3\)-critical as removing any edge leaves a tree which is \(2\)-colourabe.

\(K_n\) is \(n\)-critical.
Proof. Connectivity if \(G\) has \(m>1\) connected components \(G_1, \ldots, G_m\), then \[\chi(G) = \max\{\chi(G_1), \ldots, \chi(G_m)\}\] since we can colour them independently. Let \(G_s\) be a connected component with minimal chromatic number, i.e. \[\chi(G_s) \leq \chi(G_t) \quad \forall t \in \{1,\ldots,m\}.\]
Then \[H = G - G_s \subset G\] is a strict subgraph, but \[\chi(H) = \max \{ \chi(G_t) : t \neq s \} = \chi(G),\] so \(G\) is not critical.
Minimum degree: let \(G\) be \(k\)-critical and suppose (seeking contradiction) that some vertex \(v \in G\) has degree \(d(v) \leq k-2\).
Since \(G\) is \(k\)-critical, the proper subgraph \(G-v\) is \((k-1)\)-colourable. Let \[\beta : V \setminus \{v\} \to \{1, \ldots, k-1\}\] be a colouring of \(G-v\).
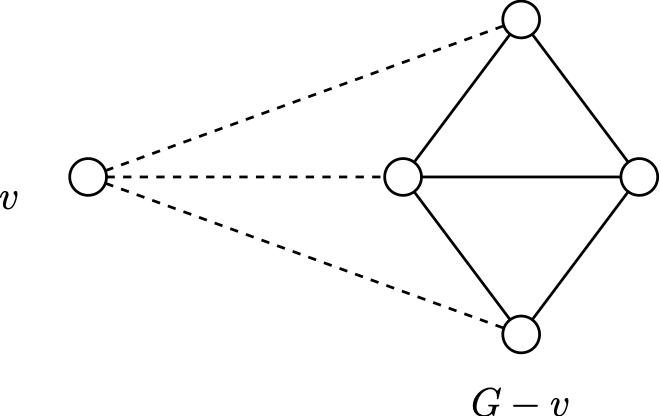
(fewer than \(k-1\) edges)
Now, in \(G\) \(v\) is adjacent to at most \(k-2\) vertices, so there is at least one colour in \(\{1,\ldots,k-1\}\) not used on a neighbour of \(v\) in the colouring \(\beta\). Give this colour to \(v\) to extend \(\beta\) to a \((k-1)\)-colouring of \(G\). Contradiction!
Proof. Write \(k = \chi(G)\). Not all subgraphs \(H\) are \(k\)-critical but at least one must be (remove edges from \(G\) till you can \((k-1)\)-colour), so \[\begin{aligned} 1 + \max_{H \subseteq G} \delta(H)&\geq 1+ \max \{\delta(H) : \text{$H \subseteq G$ is $k$-critical}\}\\ &\geq 1+ (k-1) \\ &= \chi(G). \end{aligned}\]
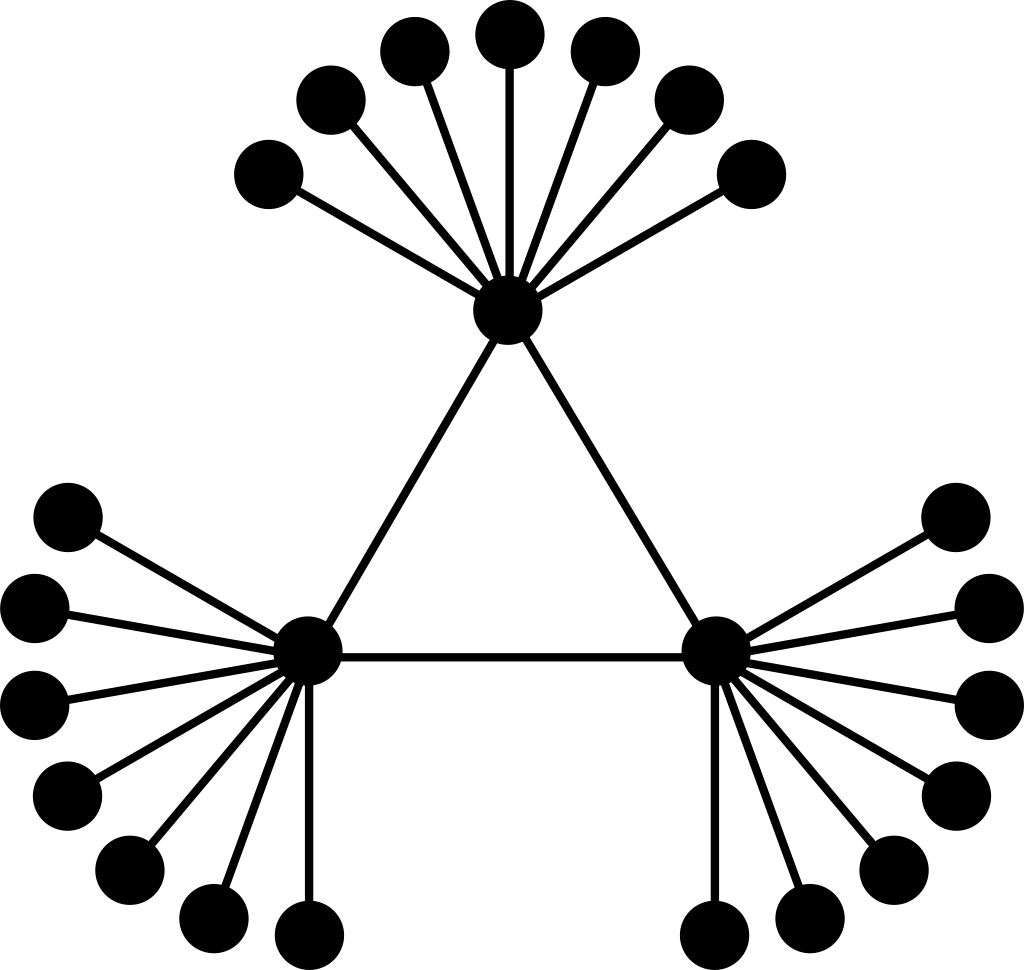
Here \(|E|=24\) so 5.3 gives \(\chi\leq 7\), and \(\Delta=9\) so 5.4 gives \(\chi\leq 10\). In fact \(\chi=3\). You can see this using 5.7 if you note that the only subgraph not containing a vertex of degree 1 or less is the triangle, which has \(\delta=2\).
In general, an \(n\)-vertex graph has \(2^n\) subgraphs, and you need to be able to somehow check the minimum degree of all of them to make use of this bound. This seems impossible, but can sometimes be easy to do when your graph has a property that is inherited by all subgraphs which allows you to estimate the minimun degree - we will see an example of this in the chapter on drawing.
5.4 Spectral bound
Recall that bipartite graphs can be characterised by their eigenvalue spectrum. Well, it turns out that we can bound the chromatic number in general by a function of the left-most and right-most eigenvalues.
Proof. Recall from Theorem 1.8 that for any vector \(\boldsymbol{w} \in \mathbb{R}^n\) we have \[\begin{aligned} \lambda_n \sum_i w_i^2 \leq \sum_{i,j} A_{ij} w_i w_j. \qquad (*) \end{aligned}\]
Let \(\boldsymbol{v}\) be an eigenvector of \(A\) with eigenvalue \(\lambda_1\) and \[\sum_i v_i^2 = 1.\]
Let \(\beta\) be a \(k\)-colouring of \(G\). For each colour \(c \in \{1, \ldots, k\}\), define a vector \(\boldsymbol{u}_c\) with entries \[\begin{aligned} u_{ci} = v_i (1-k \delta_{\beta(i),c}) = \begin{cases} v_i(1-k) & \text{if $\beta(i)=c$}\\ v_i & \text{if $\beta(i) \neq c$} \end{cases} \end{aligned}\]
We compute \[\begin{aligned} \sum_c u_{ci} u_{cj} &= \sum_c v_i v_j (1-k \delta_{\beta(i),c}) (1 - k \delta_{\beta(j),c})\\ &= v_i v_j \sum_c (1-k \delta_{\beta(i),c} - k \delta_{\beta(j),c} + k^2 \delta_{\beta(i),c} \delta_{\beta(j),c})\\ &= v_i v_j (k-k-k+k^2 \delta_{\beta(i),\beta(j)}) \\ &= v_i v_j k (k \delta_{\beta(i),\beta(j)} - 1)\end{aligned}\]
Therefore \[\sum_{c,i} u_{ci}^2 = \sum_i v_i^2 k (k-1) = k(k-1)\] and \[\begin{aligned} \sum_{c,i,j} A_{ij} u_{ci} u_{cj} &= \sum_{i,j} A_{ij} v_i v_j k (k \delta_{\beta(i),\beta(j)} - 1) \\ & \text{since $A_{ij} \beta_{\beta(i),\beta(j)}=0$}\\ &= -k \sum_{i,j} A_{ij} v_i v_j \\ &= -k \lambda \sum_i v_i^2 \\ &= -k\lambda_1 \end{aligned}\]
Plugging into \((*)\) we find \[\begin{aligned} \lambda_n k(k-1) &= \sum_c \left( \lambda_n \sum_i u_{ci}^2 \right) \\ &\leq \sum_{c,i,j} A_{ij} u_{ci} u_{cj}\\ &= -k \lambda_1, \end{aligned}\] so \[\begin{aligned} & \lambda_n (k-1) + \lambda_1 \leq 0 \\ &\Rightarrow k \geq 1 - \dfrac{\lambda_1}{\lambda_n}.\end{aligned}\]