Research

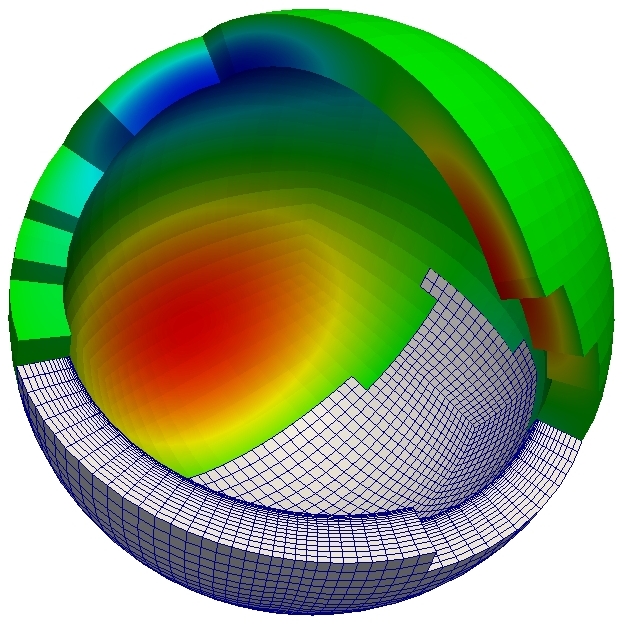
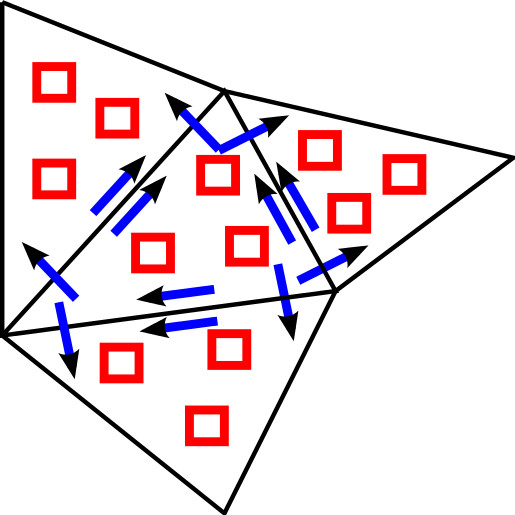
One of the main topics of my current research is the efficient implementation of fast solvers for elliptic partial differential equations (PDEs) in atmospheric modelling. For the resolutions that can be achieved today, modern algorithms have to be implemented on massively parallel supercomputers, such as HECToR (the UK's national supercomputing resource) or TITAN (currently the second fastest computer in the world according to the top 500 list [Nov 2013]).

I have a strong interest in emerging computer architectures and the application of Graphics Processing Units (GPUs) to problems in atmospheric modelling; our efficient GPU implementation of an two iterative solvers (preconditioned Conjugate Gradient and geometric multigrid) for highly anisotropic PDEs is described in [Müller et al. (2013b)] and [Müller, Scheichl, Vainikko (2015)].

I demonstrated the scalability of our solvers for problems with more than 10¹⁰ degrees of freedom on up to 65536 CPU cores [Müller, Scheichl (2014)]. On TITAN we solved a PDE with 5·10¹¹ unknowns in 1 second and achieved a performance of nearly one PetaFLOP, which is very good for a memory bound application [Müller, Scheichl, Vainikko (2015)]. In total we used 16384 GPUs with more then 40 million CUDA cores. The most successful solver is a bespoke geometric multigrid algorithm which we optimised for this particular problem.

Multigrid solver have also been implemented for more challenging mimetic (mixed) finite element discretisations in the Firedrake framework [Mitchell, Müller (2016)]. Performance measurements on the ARCHER supercomputer have demonstrated that the performance of a bespoke tensor-product geometric multigrid solver is comparable to that of the Boomer AMG implementation.

I also implemented an optimised geometric multigrid solver for the pressure correction equation in the ENDGame dynamical core of the Met Office Unified Model. First tests show that the new solver can lead to significant performance gains and it is currently tested in operational configurations of the model.

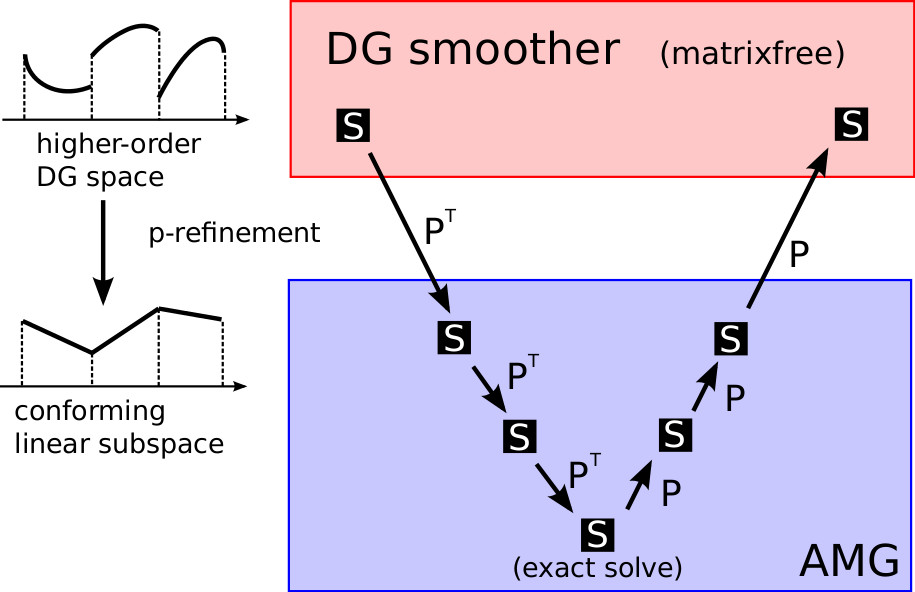
Higher order Discontinuous Galerkin (DG) methods can be used to discretise a wide range of partial differential equations in science an engineering. Applications include subsurface slow phenomena (e.g. oil- and gas- reservoir modelling, aquifers and transport in radioactive waste disposal) and numerical weather prediction. Compared to low-order discretisations, higher-order DG methods have the advantage of locality and very high computational intensity, in particular if a sum-factorisation approach is used. This makes optimal use of modern computer architectures, which can execute a very large number of floating point operations, but are slow in loading data from memory.

However, the solution of elliptic PDEs requires the inversion of small dense matrices in the block-smoother, and traditionally those matrices need to be assembled and inverted, which counteracts the advantages of the matrix-free operator application.

To overcome this issue, I work with colleagues at Heidelberg University to invert the dense matrix blocks iteratively, thus recovering the advantages of the matrix-free code. Tests demonstrated the superior performance of this approach even for relatively low polynomial degrees. All code has been implemented in the EXADUNE fork of the DUNE C++ library.

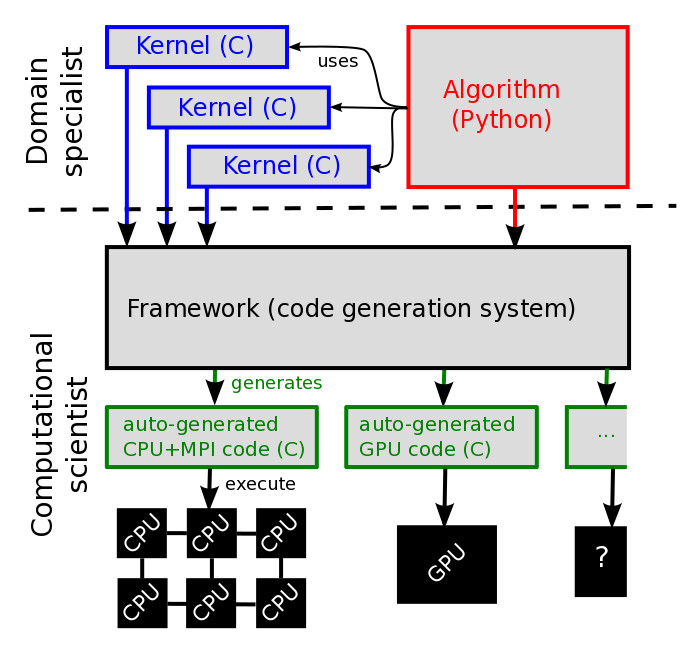
The simulation of large numbers of particles with Molecular Dynamics (MD) algorithms is a key tool in computational chemistry and physics. To extract physically meaningful data requires implementations on massively parallel computer architectures. In a diversifying hardware landscape (manycore CPUs, GPUs, Xeon Phi, ...) it is increasingly difficult for the domain specialist (computational physicist/chemist) to be an expert in the low-level optimisation of their codes. This makes the implementation of efficient yet portable MD codes for modern parallel computers very challenging.

To overcome this issue, we developed a Python code generation framework [Saunders, Grant, Müller (2017a)], [Saunders, Grant, Müller (2017b)] inspired by the PyOP2 ``Separation-of-Concerns`` approach for related problems in the solution of grid-based PDEs. The domain specialist describes the fundamental interaction between particle pairs as a short C kernel, and this is then executed over all particles pairs. Since the allowed kernels are very general, this also allows the easy implementation of structure analysis codes and with increasing data volumes this aspect becomes more important.

Image source: Árni Friðriksson (Own work) [CC-BY-SA-3.0 or GFDL], via Wikimedia Commons

As a scientist in the Met Office Atmospheric Dispersion group (November 2009 - August 2011) I contributed to the development of the NAME dispersion model, which is used for research applications and operational prediction of the spread and transport of atmospheric pollutants. The model was used for the operational forecast of the spread of volcanic ash in the European airspace following the 2010 and 2011 eruptions of Eyjafjallajökull and Grimsvotn. In particular I was responsible for the OpenMP parallelisation of the NAME model and my work lead to a significant reduction of the model runtime as described in [Müller et al. (2013a)].

During my time at the Met Office I was also involved in the development of a new operational emergency response system for accidents such as volcanic eruptions or nuclear accidents.

Together with Prof. Rob Scheichl and Dr. Tony Shardlow I co-supervise an PhD project on the application of multilevel Monte-Carlo methods in atmospheric dispersion modelling (see ↝ Teaching and Supervision). The improved time stepping methods which are developed and implemented in this project lead to significant speedups, see [Müller, Scheichl, Shardlow (2014)] and [Katsiolides et al. (2016)].

During my PhD at the University of Edinburgh (September 2006 - August 2009) I investigated the interactions of particles on a much smaller scale: I used and extended a Python/Fortran MPI code for calculating the gluonic corrections to a heavy meson decay. Due to the heavy mass of the decaying b-quark, an effective theory is used and the automated perturbation theory on the lattice [Hart et al. (2009)] and the resulting integrals are evaluated using Monte-Carlo methods. As the calculations are computationally demanding, it is important to use efficient implementations. Results for several observables which play a role in the search for new effects beyond the Standard Model of Particle Physics can be found in [Müller et al. (2009)], [Horgan et al. (2009)], [Müller, Hart, Horgan (2011)].

In my diploma thesis at the University of Bonn (Jul 2005 - Jul 2006) I used Chiral Perturbation Theory to calculate T-odd correlations in radiative Kaon decays [Kubis et al. (2007)], [Müller, Kubis, Meißner (2006)]. Again these calculations are important to compare experimental results to theoretical predictions.