Improving Next Generation Weather- and Climate Prediction Models

In my current role as a PostDoc at the University of Bath I am part of the Met Office led GungHo! project, which aims to develop a new dynamical core for the Unified Model (UM). The model is used both for short term weather prediction and long term climate simulations and the dynamical core is an important component of the code as it solves the equations of large scale fluid dynamics (the Navier Stokes equations). To improve the accuracy and reliability of weather forecasts and climate simulations, the model resolution is continuously increased to capture phenomena at smaller scales such as localised thunderstorms and winter snow (see article on Met Office webpage). The aim of the GungHo! project is to increase the global resolution substantially (to around one kilometer), which leads to significant computational challanges due to the increased data volume that needs to be processed in a very short time - tomorrow's weather forecast would not be very useful if it took a week to produce it!

Fast Elliptic solvers for numerical models of the atmosphere

[with Rob Scheichl (Bath), Stephen Pickles (STFC)]

Together with Prof. Rob Scheichl I am working on an efficient and scalable implementation for the elliptic solver of the pressure correction equation which arises in implicit time stepping in the dynamical core of the model. This partial differential equation (PDE) has to be solved at every model time step and it is important to use an algorithmically optimal solver such als multigrid or a suitably preconditioned Krylov subspace method. As the problems that are solved are large (more than 10¹⁰ degrees of freedom per atmospheric variable), the implementation has to scale well to large processor counts for 10⁵-10⁶ computing units.

Massively Parallel Scaling tests

Recently we tested the performance and scalability of set of solvers from existing and well established numerical libraries such as hypre and DUNE. In addition we wrote and optimised our own bespoke matrix-free solvers which exploit the characteristics of the pressure correction equation such as a very strong coupling in the vertical direction [Müller, Scheichl (2014)]. We found that for a representative model equations a geometric multigrid solver based on the Tensor-product idea in [Börm and Hiptmair, Num. Alg., 26 (2001), 219-234] gave the best results. The figure on the right shows the total solution time for a representative model equation for a range of different solvers, including one-level Krylov subspace methods, AMG solvers from DUNE and hypre and for the bespoke geometric multigrid code. The largest problem we solved on 65536 processor cores has 3.4⋅10¹⁰ degrees of freedom.

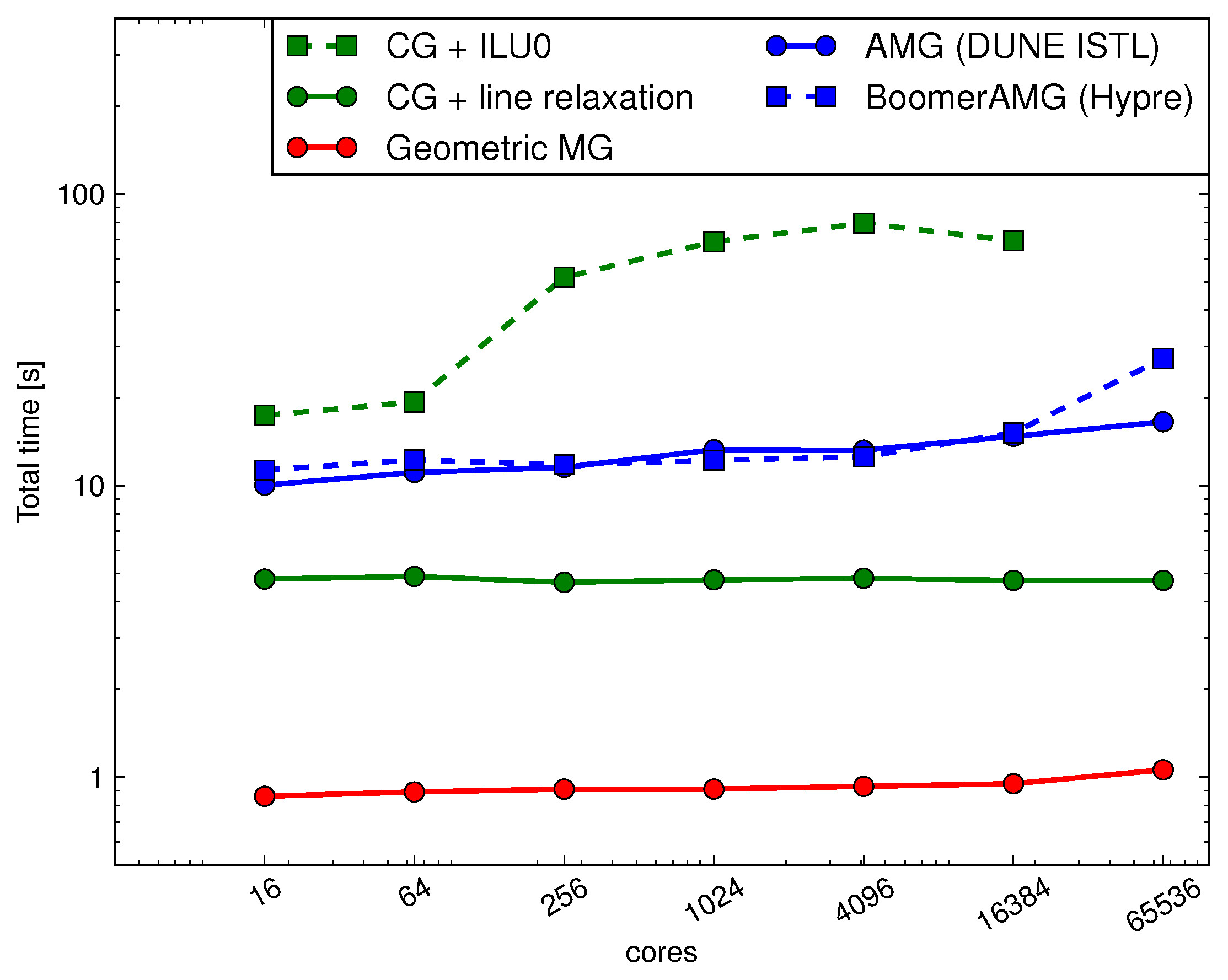
Weak scaling of the total solution time for a representative model PDE for the pressure correction equation encountered in NWP models.

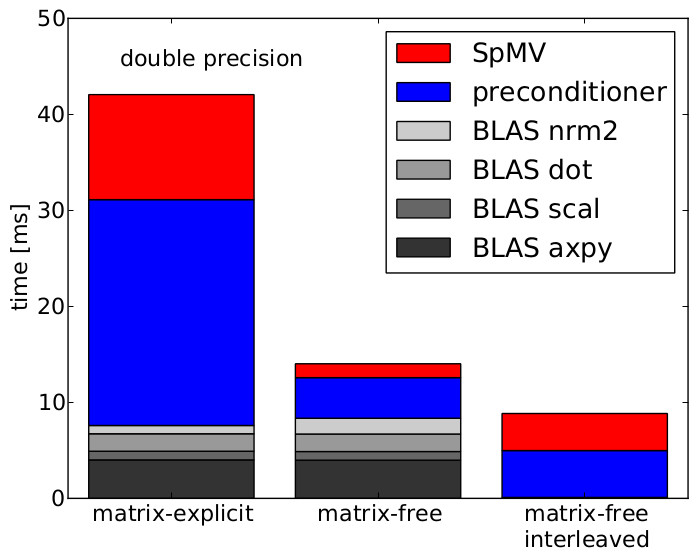
Time per iteration for different GPU solver implemetations. Our optimised matrix-free implementation is shown on the right.

Elliptic Solvers on GPUs

[with Sinan Shi, Xu Guo (EPCC), Kait Kasak, Eero Vainikko (Tartu)]

Recently Graphics Processing Units (GPUs) have received a lot of attention in all areas of Scientific Computing because of their excellent performance and power efficiency.
As part of an MSc student project with the Edinburgh Parallel Computing Centre (EPCC) we implemented a Preconditioned Conjugate Gradient (PCG) solvers for the model equation using the CUDA programming model on nVidia Fermi GPUs. On GPUs it is vital to optimise the memory access pattern and cache reusage, both of which have to be controlled explicitly by the programmer. We achieved this by using a matrix-free implementation, which exploits the tensor-product structure of the problem to recalculate the matrix stencil instead of reloading it from memory. We also fused some of the computational kernels in the PCG algorithm to optimise cache efficiency. With our optimised implemementation we could achieve a total global memory bandwidth (which is a good measure of the efficiency for memory bound applications) of around 25%-50% percent of the peak value and could solve the equation around 50 times faster than a sequential code on a Sandybridge CPU [Müller et al. (2013b)]. The figure on the left shows the time per iteration for a PCG solver for different implementations. It clearly demonstrates the superior performance of our bespoke matrix-free code.

Massively Parallel Scaling tests on very large GPU clusters

[with Eero Vainikko (Tartu), Benson Muite (KAUST & Tartu)]

For problem sizes which are encountered in next generation weather prediction models, PDEs with up to 10¹¹ unknowns need to be solved. To achieve this, we parallelised our matrix-free solver across multiple GPUs by using the Generic Communication Library (GCL, Mauro Bianco et al.). Optimal algorithmic performance is crucial and we developed a tensor product geometric multigrid solver in addition to the CG algorithm. The multigrid solver converges in a much smaller number of iterations and reduces the overall solution time significantly. We ran our code on up to 16384 GPUs of the TITAN (currently the second fastest computer in the world according to the top 500 list [Nov 2013]) and on the EMERALD cluster. With the multigrid solver we are able to solve a PDE with 0.5·10¹¹ unknowns in around 1 second (reducing the residual by five orders of magnitude). We achieved a floating point performance of just under one PetaFLOP/s. As the code is memory bound, a more representative number for sparse linear solver is the utilised global GPU memory bandwidth. Here we were able to achieve between 25% and 50% which is a sizeable fraction for a memory bound code. The figure on the right shows a weak scaling plot of the total solution time for increasing problem sizes on the TITAN and EMERALD GPU clusters. We also compare the results to a CPU implementation on HECToR; the GPU solver is about a factor 4 faster in a socket-to-socket comparison (comparing TITAN's K20X GPUs to the 16 core AMD Opteron chips on HECToR). More details can be found in [Müller, Scheichl, Vainikko (2015)].

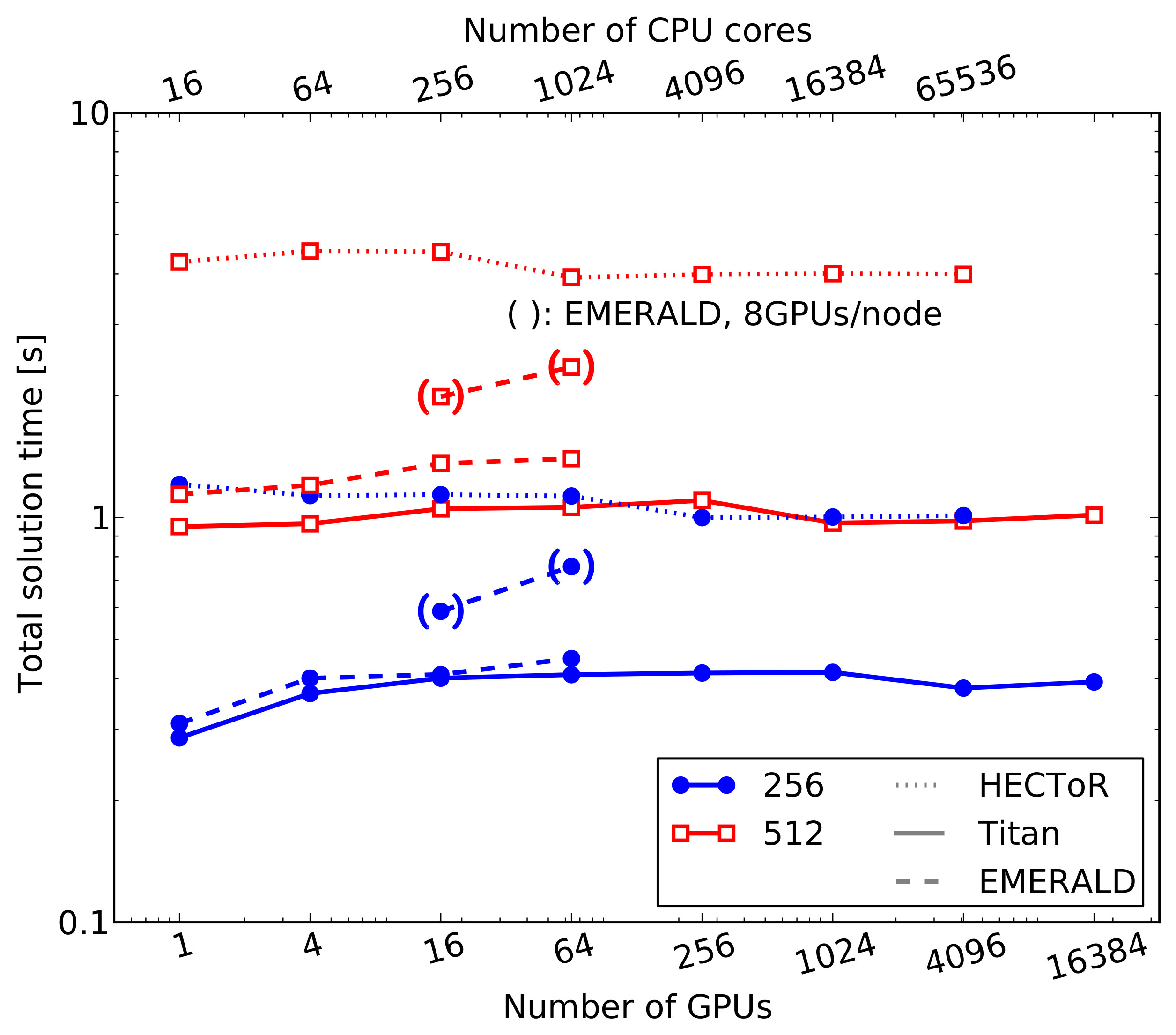
Weak scaling of the total solution time for the geometric multigrid solver and two different local problem sizes (256x256x128 and 512x512x128) on TITAN and EMERALD. A socket-to-socket comparison to the CPU implementation on HECToR is also shown.

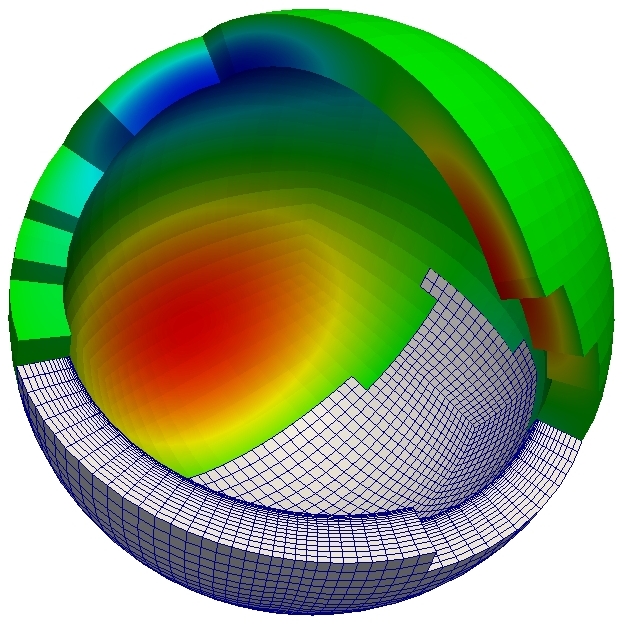
DUNE Implementation of Multigrid Solvers on Tensor-product grids

[with Rob Scheichl (Bath), Andreas Dedner (Warwick)]

The computational grids encountered in the GungHo! project have a very specific structure and can be written as the tensor-product of a semi-structured two dimensional grid on a sphere and a one-dimensional vertical grid. The Distributed and Unified Numerics Environment (DUNE) provides a C++ framework for implementing grids of this type, optimal performance is achived by C++ templates and generic metaprogramming. Together with Dr. Andreas Dedner (Warwick), who is one of the DUNE core developers, we implemented a bespoke geometric multigrid solver in the DUNE framework [Dedner, Müller, Scheichl (2016)] and demonstrated its performance and parallel scalability for different atmospheric test problems. The figure on the right shows a hierachy of grids on a sphere.

A fast geometric multigrid solver for the Met Office Unified Model

[with Markus Gross (Met Office) and Rob Scheichl (Bath)]

The Met Office is current developing a new dynamical core (codenamed ENDGame) for the Unified Model. As the model uses semi-implicit semi-Lagrangian time stepping, this requires the frequent solution of an eliptic PDE for the pressure correction and currently a preconditioned BiCGSTab solver is used for this. Based on the ideas in [S.D. Buckeridge and R. Scheichl: Numerical Linear Algebra with Applications, 17:325-342 (2010)] I implemented an optimised geometric multigrid solver based on vertical line relaxation and horizontal semi-coarsening and tested it together with Markus Gross at the Met Office. Currently the solver is being integrated it into the full model which is expected to become operational in 2014. First tests show very promising performance gains compared to the current Krylov subspace solver.

The figure on the left shows the convergence history of both solvers for an N512 run with 1024 x 768 x 70 grid points an demonstrates that the number of iterations can be reduced considerably with the multigrid algorithm. Both runs were carried out on 256 cores of the HECToR supercompter; on this architecture one multigrid iteration is not significantly more expension that one iteration of BiCGStab.

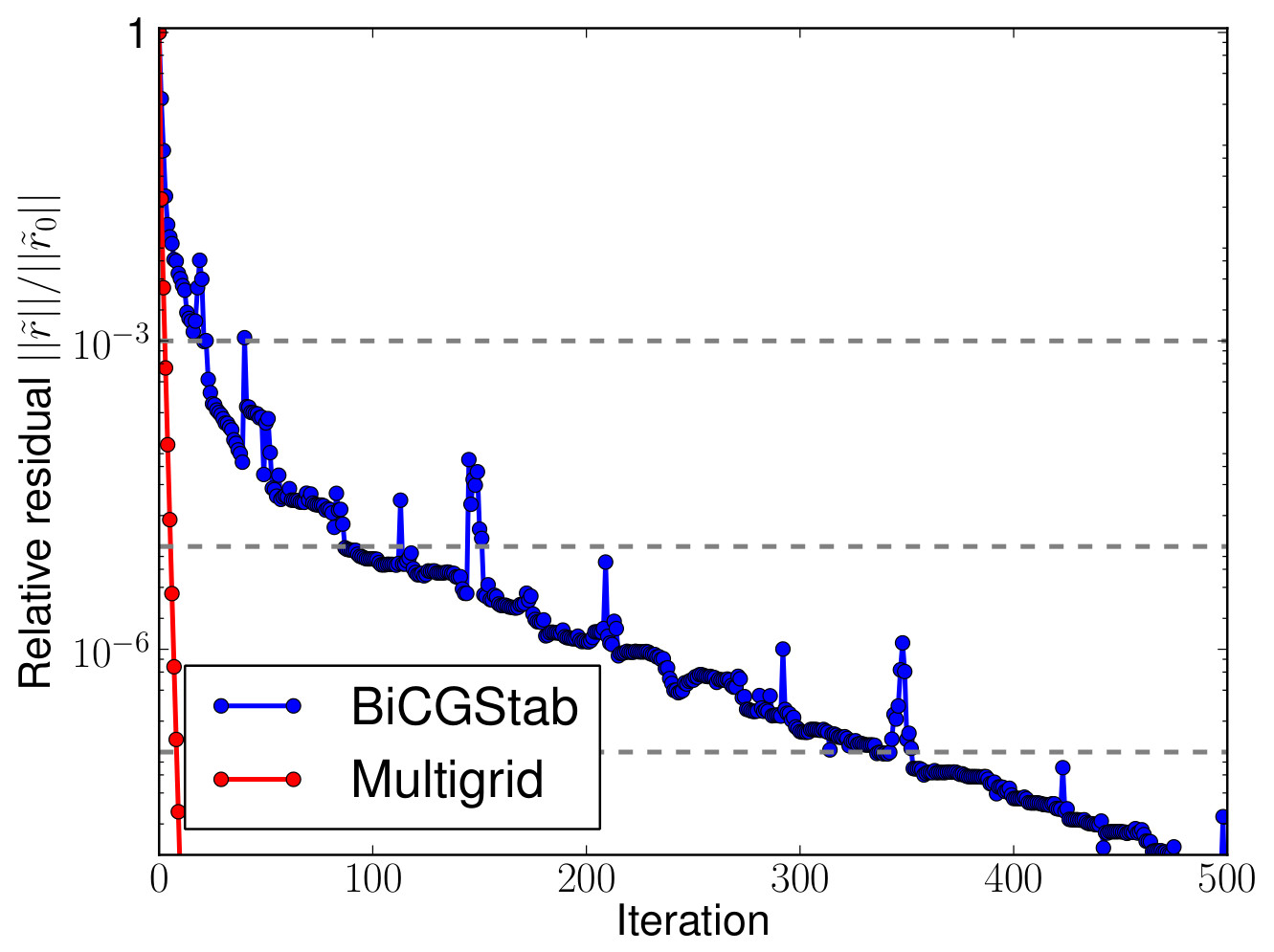
Convergence history of the current BiCGStab solver and the optimised multigrid solver