Plotting and Arrays¶

You have now seen the basic Python language (“syntax”) and programming methods.
These basic building blocks can be built-up to construct advanced programs for things such as:

solving the equations for engineering problems;
simulating the behaviour of constructions and other designs;
optimising structures, energy flows or other problems;
analysing data from measurements in order to present the results.

For the last item you will need some extra tools, including how to plot your results in high-quality figures and how to load your data from files and save the results.

In this section we will learn how to plot professional quality figures and save them for use in reports and presentations.
This section covers 2D plotting in this section but 3D can be seen in the supplementary notes.

General advice on working through these notes:¶

New functions new methods of manipulating data will be introduced as they are needed.

Keep a file or notebook to make a note of the most useful functions and methods for you to look up when you need them, as it is impossible to remember everything.
For things you use less frequently look them up on the internet or in the manuals by searching for what you want to do and the keywords “Python” or “Matplotlib” along with any other snippets you remember.
- Most programmers consult the online guides frequently.

Importing Modules and Accessing Attributes¶

In order to manipulate numerical data effectively we need to use a new data type called a numerical array.
These can be used more mathematically than lists and behave a little differently.

Arrays and plotting functions are imported from external libraries, in the same way we have already seen for the math and numpy libraries.

Matplotlib¶

Matplotlib, and particularly its plotting capabilities in pyplot, are used to create publication quality figures of functions and data. The functionality is vast, and you will need to refer to the documentation frequently until you are familiar with what you need from it and the details of how it is used:
https://matplotlib.org/stable/tutorials/introductory/usage.html.
Most of the functionality we will be using are contained in the pyplot functionality of Matplotlib, which is normally accessed using:

import matplotlib.pyplot as plt

The various plotting tools and ways of specifying figure attributes are then accessed using the syntax:

plt.ATTRIBUTE(ARGUMENTS)

The Basics of Plotting¶

In its simplest terms the plot() function in pyplot takes a list of \(x\) values and plots each one on the \(x-\)axis against a corresponding \(y-\)value from a list of \(y\) values of the same length.

This is demonstrated for the squares of \(x=[1,2,3,4]\) below:

import matplotlib.pyplot as plt

xvals = [1, 2, 3, 4]
yvals = [1, 4, 9, 16]

plt.plot(xvals, yvals)

plt.show()

However: there are two main methods of plotting figures, so the online documentation can sometimes be confusing at first.

See the guide here for the alternative way of making figures as used above. Although this may seem simpler at first (and looks like other languages such as MATLAB) the method used below is more flexible and “object oriented”.

Creating a Figure¶

The plt.subplots function returns two things: a figure canvas to construct a figure on, and a set of axes to draw specific plots on.

The fig object has .ATTRIBUTES for changing things such as the figure title, axis labels and decorations
The ax object has .ATTRIBUTES such as functions for specific plot types etc.

fig, ax = plt.subplots()

Once you have some axes (on a figure) you can start drawing things directly on them.

Example: Square Wave¶

To plot a “square wave” that switches between the values \(y=+1,-1,+1,-1,\dots\) every \(\pi\) radians:

import matplotlib.pyplot as plt

# create a single set of axes on a figure
fig, ax = plt.subplots()

pi=3.14
xvals = [-2*pi, -pi, -pi, 0, 0, pi, pi, 2*pi]
yvals = [    1,   1,  -1,-1, 1,  1, -1,   -1]

ax.plot(xvals, yvals)

plt.show()

Multiple axes on the same plot¶

The possible arguments to plt.subplots() are given in the documentation here: https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.subplots.html#matplotlib.pyplot.subplots

matplotlib.pyplot.subplots(nrows=1, ncols=1, *, sharex=False, 
                  sharey=False, squeeze=True, subplot_kw=None, 
                  gridspec_kw=None, **fig_kw)

Of particular interest are the number of rows nrows and columns ncols of axes on the figure.
If you don’t specify there will only be a single set of axes as above, but if you give two values as arguments they stand for the number of rows and number of columns.
The ax object will then be a [list] of axes or a set of axes, depending on how you unpack the returned values:

Try out the following examples below to see what they do¶

Two rows (one column by default) and the variable ax contains a list of two axes ax[0] and ax[1]¶

fig, ax = plt.subplots(2)

a 2x2 grid of axes using the variable `axs` for multiple Axes: axs = [axs[0], axs[1], axs[2], axs[3]]¶

fig, axs = plt.subplots(2, 2)

Each axis has its own variable name, for multiple Axes, here ax1 and ax2¶

fig, (ax1, ax2) = plt.subplots(1, 2)

# YOUR CODE HERE

Numpy and Numerical Arrays¶

Lists are useful but it can be fiddly to perform mathematical operations for each element, e.g.::

b = [3*sin(x)**2+10 for x in a]

Also multiplying a list by a number is interpreted as adding the list to itself that number of times:

alist = [1, 2, 3]
print(alist+alist)
print(alist*3)

[1, 2, 3, 1, 2, 3, 1, 2, 3]```

Another data type can be imported with the Numerical Python (NumPy) module that behave in a more mathematically logical way.

Numpy¶

NumPy is a Python library that provides efficient operation on arrays of data.
NumPy stores data in what are called numerical arrays, along with many functions for generating and methods for manipulating them.

It is usually imported using the alias np:

import numpy as np

You can then get help by using the help(MODULE.THING) command, for example type:

help(np.random)

To see the help manual on the random functions in NumPy.

Converting Lists to Arrays¶

An array looks like a list but it is a NumPy N-Dimensional Array (in this case 1D).

NumPy arrays have element-by-element (elementwise) operations, which is more logical mathematically:

import numpy as np

alist = [1, 2, 3, 4]
ary = np.array(alist)

print(ary+ary)
print(ary*ary)
print(ary**3)

Plotting can be done on arrays the same as with lists:

import matplotlib.pyplot as plt
import numpy as np


xvals = np.array([1,2,3,4,5,6,7,8,9,10])
xsquared = xvals**2

fig, (ax1, ax2) = plt.subplots(1, 2)

ax1.plot(xvals, xsquared)
ax2.plot(xvals, np.sqrt(xvals))

fig.show()

NumPy also contains functions that can act directly on all the elements of an array (unlike those in the math library`)

Generating Arrays with `arange()`¶

NumPy can generate arrays directly using the function arange():

import numpy as np

a = np.arange(1, 8)
print(a)
print(a**2)

The arange function can also use fractional values

The syntax is range(VAR1,VAR2,STEP), where the values created are those between VAR1 and VAR2, including VAR1 but not VAR2:

import numpy as np

a = np.arange(-1, 1, 0.5)

print(a)

Note: the second value is not included in the array, so to get around this the value needs to be slightly above the required end-point.

Exercise: Create an array that goes from `-2` to `2` in steps of `0.2` and includes the numbers `-2`, `0` and `2`¶

# YOUR CODE HERE

Note: Sometimes the arange function returns the values in scientific notation, as above.

This is due to the central value being very close to zero but not quite (due to precision accuracy).

One solution to this is to use the .round() function method built in to arrays:

import numpy as np
a = np.arange(-2, 2.1, 0.2)

print(a.round(1))

Generating Arrays with `linspace()`¶

The arange function is useful when we want an array of numbers with a fixed spacing. However, in some applications we might want an array that starts and ends at fixed values but has a certain number of steps in between.

For this we can use the linspace function from NumPy, which stands for “linear spacing”.
Type help(np.linspace) to read more about it:

import numpy as np
pi = np.pi

a = np.linspace(-pi, pi, 5)
print(a)

This has returned 5 values in total, including both the start value \(-\pi\) and end value \(\pi\).
That is, with x=linspace(a,b,n) \(a \leq x \leq b\) (unlike with x=arange(a,b,dx) where \(a \leq x < b\)).

Both linspace and the previous arange function are very useful when plotting mathematical functions.

Plotting using Arrays¶

Arrays can be used to generate the \(x\) and \(y\) values for plotting against each other, and the maths on arrays makes it much easier to generate \(y\) values from an array of \(x\) values:

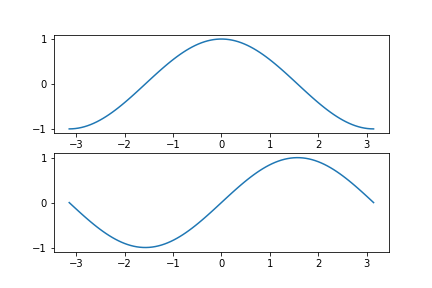
Exercise: Create an array of 100 values from \(-\pi\) to \(\pi\) using `linspace()` for x-values, create a plot with two axes (two rows and one column), one above the other and plot \(\cos(x)\) on the top `ax1` and \(\sin(x)\) on the bottom `ax2`:¶

import numpy as np
import matplotlib.pyplot as plt
pi = np.pi
sin = np.sin
cos = np.cos

#xvals = ???  
#cosx = ???
#sinx = ???
# YOUR CODE HERE

#create your plot canvas and pair of axes (ax1, ax2) (see examples further up in the notes)
# YOUR CODE HERE

# plot cos(x) on ax1 and sin(x) on ax2
# YOUR CODE HERE

fig.show()

Expected Result:

Click for solution

Changing the Plotting Attributes¶

Plotting Styles¶

We can change the plotting style (and many other features) using extra arguments to the subplots and plot functions.
The plot attributes can be given as keyword arguments after the x-values and y-values.
The arguments are given as strings and consist of either a symbol to specify a marker or line type or the colour
(spelled using the American spelling color, without a “u”):

import numpy as np
import matplotlib.pyplot as plt

xvals = np.arange(11)
yvals = xvals**2

# set some x and y dimensions (in inch !!!)
dims = (8,8)
fig, ax = plt.subplots(figsize=dims) # specify the size of the figure

ax.plot(xvals, yvals, linestyle='--', marker='o', color='red')

plt.show()

Use help(ax.plot) to see what else is available and experiment with line styles and points etc.
Also refer to the many online resources for matplotlib as well as the extra cheat-sheet.

help(ax.plot)

Multiple Plots on the same axis¶

The following example shows that we can plot more than one function on the same graph. A different colour is automatically used for each function.

import numpy as np
import matplotlib.pyplot as plt
pi = np.pi

fig, ax = plt.subplots()

xs = np.linspace(0, 2*pi, 50)
ys = np.sin(xs)
zs = np.cos(xs)

ax.plot(xs, ys)
ax.plot(xs, zs)

plt.show()

Labels and Legends¶

We next improve the plot by adding labels for the horizontal and vertical axes and we add a legend as well as a title.

Add lines between ax.plot() and fig.show() to include the following functions: ax.set_xlabel(<TEXT>), ax.set_ylabel(<TEXT>), ax.set_title(<TEXT>) and ax.legend().
The optional keyword argument size=12 can be used to specify the text size.

The figure should look like the example below the code block.
Use the help() function if you are unsure.

import numpy as np
import matplotlib.pyplot as plt
pi = np.pi


xs = np.linspace(0, 2*pi, 50)
ys = np.sin(xs)
zs = np.cos(xs)

fig, ax = plt.subplots()

ax.plot(xs, ys, label="sin(t)")
ax.plot(xs, zs, label="cos(t)")

# YOUR CODE HERE

fig.show()

help(ax.set_xlabel)

Expected Result: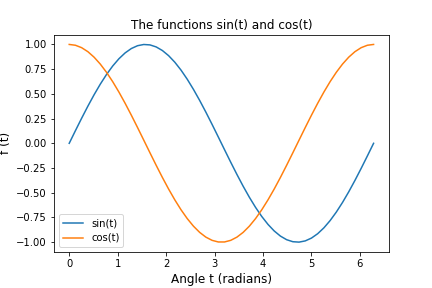

Click for solution

Other features can be changed, such as defining the x and y ranges using the function:

ax.set(xlim=(XMIN, XMAX), ylim=(YMIN, YMAX))

Where XMIN, XMAX, YMIN and YMAX are replaced by values.

The position of the legend can also be specified using one of four built-in position numbers or a pair of numbers in brackets for the relative position on the plot. Other options are available such as "best", which can be found in the help manual.

Copy the code from above to the cell below and use the ax.set() function to limit the range to \(0\leq x \leq\pi\) and \(0 \leq y \leq 1\)
Also use the loc=(XPOS,YPOS) argument in legend() to specify the legend position relative to the axes. (You may need to experiment with some values between 0 and 1)
Changing the font size can be done individually as above, or for the whole plot using the command plt.rc('font', size=14), which changes the “resource configuration” for matplotlib generally.

import numpy as np
import matplotlib.pyplot as plt
pi = np.pi
plt.rc('font', size=12)

# YOUR CODE HERE

fig.show()

Expected Result: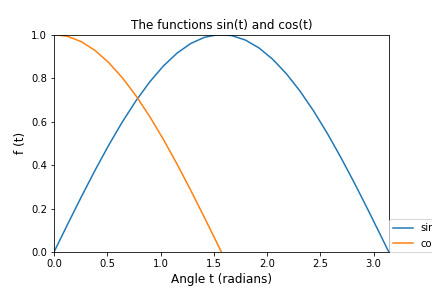

Click for model code

AR10366 (Computer Applications): Programming in Python

Plotting and Arrays¶

General advice on working through these notes:¶

Importing Modules and Accessing Attributes¶

Matplotlib¶

The Basics of Plotting¶

Creating a Figure¶

Example: Square Wave¶

Multiple axes on the same plot¶

Try out the following examples below to see what they do¶

Two rows (one column by default) and the variable ax contains a list of two axes ax[0] and ax[1]¶

a 2x2 grid of axes using the variable axs for multiple Axes: axs = [axs[0], axs[1], axs[2], axs[3]]¶

Each axis has its own variable name, for multiple Axes, here ax1 and ax2¶

Numpy and Numerical Arrays¶

Numpy¶

Converting Lists to Arrays¶

Generating Arrays with arange()¶

Exercise: Create an array that goes from -2 to 2 in steps of 0.2 and includes the numbers -2, 0 and 2¶

Generating Arrays with linspace()¶

Plotting using Arrays¶

Exercise: Create an array of 100 values from \(-\pi\) to \(\pi\) using linspace() for x-values, create a plot with two axes (two rows and one column), one above the other and plot \(\cos(x)\) on the top ax1 and \(\sin(x)\) on the bottom ax2:¶

Changing the Plotting Attributes¶

Plotting Styles¶

Multiple Plots on the same axis¶

Labels and Legends¶

Saving Figures to a File on Your Hard Drive¶

Finding your figures on your computer:¶

The rest of this section consists of useful practical examples for you to work through and think about.¶

Filled Charts and Plots¶

Pie Charts¶

Bar Plots¶

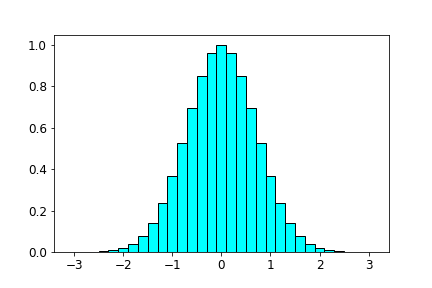
Exercise: Fill in the following code to produce a bar plot that uses np.exp(x) to create \(y=e^{-(x^2)}\) as \(y\) values:¶

Task 6¶

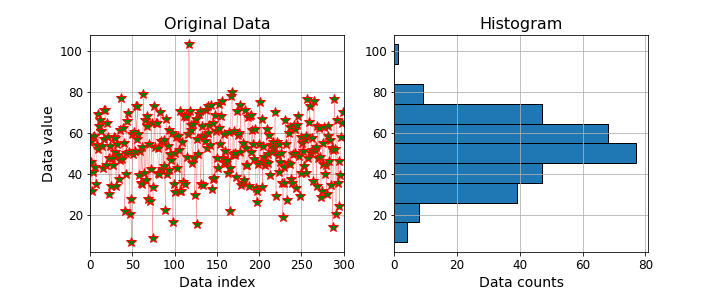
RESTART THE KERNEL before starting this exercise¶

Complete the function in the cell below that takes some \(x\) and \(y\) data and returns a figure object to display or save, then apply the function to some random data and save it.¶

Use the following steps for using the plotting functions and styles:¶

Self-help¶

Feedback cell:¶

Further Material: Creating Multiple Plots using Loops¶

Use the following example as a template to help build up the exercises below it.¶

Exercise: Fourier Series¶

Plotting the component functions¶

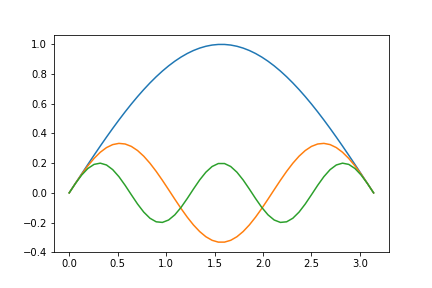
Summing the Terms¶

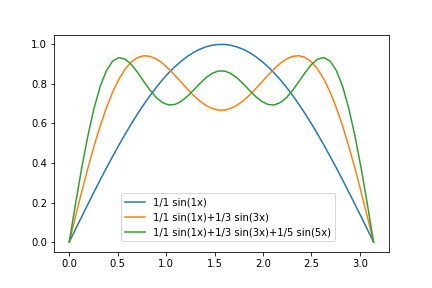
Convergence¶

Using loops with subplots¶

a 2x2 grid of axes using the variable `axs` for multiple Axes: axs = [axs[0], axs[1], axs[2], axs[3]]¶

Generating Arrays with `arange()`¶

Exercise: Create an array that goes from `-2` to `2` in steps of `0.2` and includes the numbers `-2`, `0` and `2`¶

Generating Arrays with `linspace()`¶

Exercise: Create an array of 100 values from \(-\pi\) to \(\pi\) using `linspace()` for x-values, create a plot with two axes (two rows and one column), one above the other and plot \(\cos(x)\) on the top `ax1` and \(\sin(x)\) on the bottom `ax2`:¶

Exercise: Fill in the following code to produce a bar plot that uses `np.exp(x)` to create \(y=e^{-(x^2)}\) as \(y\) values:¶