Rosa Antonia Kowalewski
About me
I am currently a PhD student at the University of Bath, in the CDT Statistical and Applied Mathematics (SAMBa).
Supervised by Karsten Matthies (Dept of Mathematical Sciences, Bath) and David Tsang (Dept of Physics, Bath) I am looking at geometry of non-conservative fluid mechanics, aiming to express the non-conservative action principle introduced by Galley (2013) in general terms of deformations (instead of explicit coordinates). The goal is to find expressions for the non-conservative potential for examples of turbulent flows in astrophysics.
I completed my Bachelor's and Master's degree in Computational Life Science at the University of Lübeck. My master's studies were specialised in image analysis.
During my studies I worked on research projects in the Cambridge Image Analysis group at the University of Cambridge, and at Laboratoire Jacques-Louis Lions at the Sorbonne Université in Paris.
My research
Projects
The following are research projects that I am or have been working on.
With different applications in theoretical physics, and image and shape analysis, the common topic is the differential geometric theory.
Geometric viewpoint of Non-conservative Action Principles
(PhD project)
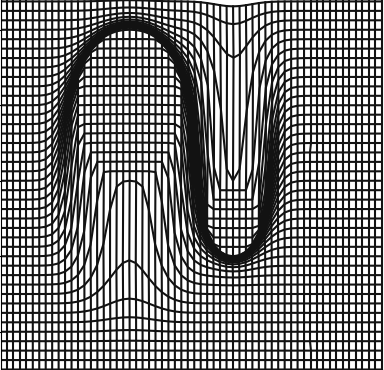
Modular Multi-Shape Registration
(Master's project)
In collaboration with Barbara Gris, Laboratoire Jacques-Louis Lions, Université Pierre et Marie Curie (Paris)
Supervised by Prof. Jan Lellmann, Intitute of Mathematics and Image Computing, Universität zu Lübeck (Lübeck)
Abstract
The deformation module approach introduced in [1] is a generic framework for integrating prior knowledge about desired deformation fields in shape and image registration.
Deformation modules allow to build diffeomorphic deformations that satisfy a given structure, for example locally affine transformations, scalings and rotations, or a combination.
The diffeomorphisms are built by integrating a flow of constrained velocity fields.
However, in applications such as modeling of respiratory motion in abdominal images for operation planning, one often encounters situations where a single deformation model is not adequate.
While it makes sense to consider diffeomorphic deformations of the seperate organs, breathing motion results in a non-smooth and possibly discontinuous displacement field at organ boundaries.
To be able to use different constrained deformations for different organs, we combine the model with a framework to introduce region boundary constraints for multiple interacting objects in a shape or image, as introduced in [2].
Deformation fields are built for each object separately, while their interaction is incorporated by constraints on the deformation of the object boundaries.
We derive theoretical results on the existence of optimal trajectories for the constrained registration problem and provide numerical results to demonstrate the potential of our approach.
Related Work
[1] Gris, Barbara. Modular approach on shape spaces, Sub-Riemannian geometry and computational anatomy. Diss. 2016.
[2] Arguillere, Sylvain. Géométrie sous-riemannienne en dimension infinie et applications à l'analyse mathématique des formes. Diss. 2014.
Documents
Thesis
Poster (presented at the European Women in Mathematics Conference 2019 in Leipzig)
Indirect Image Registration: Geodesic Shooting for LDDMM and Deep Learning Approaches
Supervised by Dr. Carola B. Schönlieb, Department of Mathematics and Theoretical Physics, University of Cambridge
In collaboration with
Ozan Öktem, KTH Royal Institute of Technology (Stockhholm)
Barbara Gris, Laboratoire Jacques-Louis Lions, Université Pierre et Marie Curie (Paris)
Abstract
In my project 'Indirect Image Registration: Geodesic Shooting for LDDMM and Deep Learning Approaches' the question was how to do registration of images where the template image is only given in the data space, e.g. as a sinogram of a CT.
I familiarized with the LDDMM model, which is based on modeling the registration as an evolution of the template image over time to match the reference image, motivated by fluid mechanics. By geodesic shooting it is possible to describe this evolution over time by only a momentum at the staring point. The optimization process to find the optimal momentum needs complicated and time-consuming calculations.
I worked out different formulations for using this approach together with a Machine Learning approach for faster, almost real-time computation.
Related Work
Chen, Chong, and Ozan Öktem. Indirect image registration with large diffeomorphic deformations. SIAM Journal on Imaging Sciences 11.1 (2018): 575-617.
Documents
Report

Prizes and Grants
WiMLDS Best Paper Award, awarded at the 5th international conference on Geometric Science of Information (GSI 2021),
for the paper "Multi-Shape registration with constrained deformations"
I received the Kovalevskaya Travel Grant, for traveling to the International Congress of Mathematicians (ICM2022) in St. Petersburg
Extracurricular Engagement
I am organising the student-led SAMBa Ethics in Maths working group on ethical topics arising mathematical research in my department.
Contact
E-Mail: rak53@bath.ac.uk
Postal Address: Dept of Mathematical Sciences
University of Bath
Bath
BA2 7AY
United Kingdom

