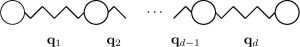
In principle, classification of a problem size as “high” or “low” depends on the amount of available memory in our computer and time. However, there are models that would require colossal numbers of unknowns for any sensible resolution in a straightforward discretisation. They arise when we need to take into account all possible realisations of a system with many “dimensions”, i.e. independent degrees of freedom. A toy example requiring minimal knowledge of mathematics and probability is described in the Summary of my former Fellowship. A rigorous mathematical model of that example is given by the Fokker-Planck equation. For simplicity, imagine a mechanical system, whose inner movement laws are prescribed by linear Ordinary Differential Equations, but the system is perturbed by the stochastic Brownian motion. The stochastic ODE reads
$$
\frac{dx_i}{dt} = \sum_{j=1}^d A_{i,j} x_j + \frac{dW_i}{dt}, \quad i=1,\ldots,d.
$$
Since \(W\) is a random process, so is \(x\), and only its statistics can be quantified, such as the probability density function. The latter is a function of all components of \(x=(x_1,\ldots,x_d)\), and obeys the Fokker-Planck equation:
$$
\frac{\partial\psi}{\partial t} = \sum_{i,j=1}^{d,d} \frac{\partial^2 \psi}{2\partial x_i \partial x_j} – \frac{\partial(A_{i,j}x_j \psi)}{\partial x_i}.
$$
This is now a Partial Differential Equation with \(d\) coordinates. Without a priory knowledge on the role of different \(x_i\), we would introduce e.g. a finite element discretisation with \(n\) degrees of freedom in each coordinate. In total we have \(n^d\) unknowns. A system \(\frac{dx}{dt} = Ax\) with \(d=100\) components might seem moderate, but \(10^{100}\) unknowns in the discretised Fokker-Planck equation cannot be even stored in memory.
Similar effect takes place in quantum models. The simplest Schroedinger equation for spin-\(\frac{1}{2}\)-only particles is an eigenvalue problem
$$
\hat H \psi = E \psi, \qquad \mbox{where}
$$
$$
\hat H = \sum_{i=2}^{d} \sum_{\mu=1}^{3} \sigma_0^{\otimes i-2} \otimes \sigma_{\mu} \otimes \sigma_{\mu} \otimes \sigma_0^{\otimes d-i}.
$$
Here, \(\sigma_0,\sigma_{\mu}\) are just \(2 \times 2\) Pauli matrices, but \(\hat H\) is a \(2^d \times 2^d\) matrix. Trying to compute the Kronecker products \(\otimes\) explicitly would result in an Out of Memory exception for as few as 30 particles on most workstations.
Another possibility is a stochastic PDE in the context of uncertainty quantification. We may have a classical diffusion equation in two or three coordinates,
$$
-\nabla a \nabla u = f,
$$
but with the coefficient \(a\) being a random field. A realisation of the coefficient may depend on several extra parameters, i.e. it is described by a multivariate function \(a = a(x,y_1,\ldots,y_d).\) As a result, the solution depends on \(y_1,\ldots,y_d,\) too.
The workaround is to avoid the “naive” discretisation with \(n^d\) unknowns. Several methods exist for that purpose. Most well-known are Sparse Grids, Monte Carlo methods, and tensor product decompositions. For further reading on the first two families you may look at Sparse Grids in a Nutshell, Dimension-Adaptive Sparse Grids, as well as tutorials on Monte Carlo and quasi-Monte Carlo techniques. In the next section we focus on the tensor decompositions.