Appendix: The Probability Integral Transform
Here is a very elegant and useful piece of probability theory. Let \(X\) be a scalar random variable with sample space \(\mathcal{X}\) and distribution function \(F(x) := \mathbb{P}(X \leq x)\). By convention, \(F\) is defined for all \(x \in \mathbb{R}\). By construction, \(\lim_{x \downarrow -\infty} F(x) = 0\), \(\lim_{x \uparrow \infty} F(x) = 1\), \(F\) is non-decreasing, and \(F\) is continuous from the right, i.e.
\[\begin{eqnarray*}
\lim_{x' \downarrow x} F(x') & = & F(x) .
\end{eqnarray*}\]
Define the quantile function
\[\begin{eqnarray}
F^-(u) & := & \inf \{ x \in \mathbb{R} : F(x) \geq u \}. \tag{4.22}
\end{eqnarray}\]
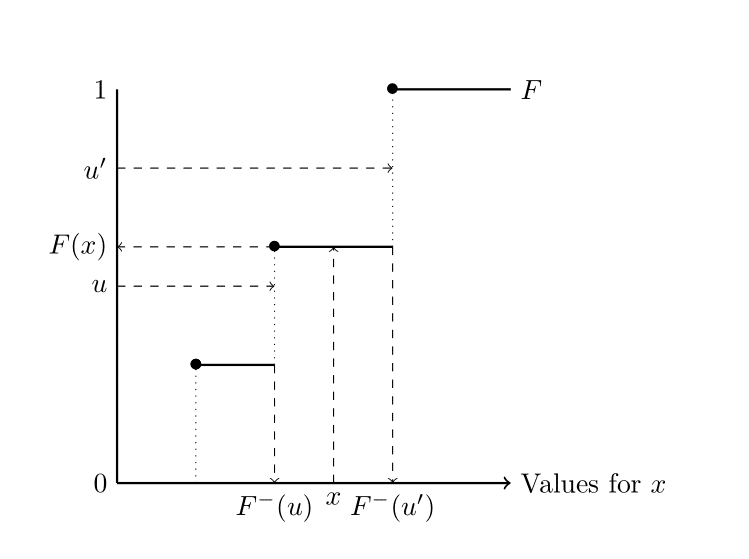
Figure 4.1: The distribution function \(F\) is non-decreasing and continuous from the right. The quartile function \(F^- = \inf \{ x \in \mathbb{R} : F(x) \geq u\}\)
The following result is a cornerstone of generating random variables with easy-to-evaluate quantile functions.
Theorem 4.10 (Probability Integral Transform, PIT) Let \(U\) have a standard uniform distribution. If \(F^-\) is the quantile function of \(X\), then \(F^-(U)\) and \(X\) have the same distribution.
Proof: Let \(F\) be the distribution function of \(X\). We must show that \[\begin{eqnarray} F^-(u) \leq x & \iff & u \leq F(x) \tag{4.23} \end{eqnarray}\] because then \[\begin{eqnarray*} \mathbb{P}(F^-(U) \leq x ) \ = \ \mathbb{P}(U \leq F(x)) \ = \ F(x) \end{eqnarray*}\] as required. Now, see Figure 4.1, it is easy to check that \[\begin{eqnarray*} u \leq F(x) & \implies & F^-(u) \leq x, \end{eqnarray*}\] which is one half of equation (4.23). It is also easy to check that \[\begin{eqnarray*} u' > F(x) & \implies & F^-(u') > x. \end{eqnarray*}\] Taking the contrapositive of this second implication gives \[\begin{eqnarray*} F^-(u') \leq x & \implies & u' \leq F(x), \end{eqnarray*}\] which is the other half of equation (4.23). \(\Box\)
Theorem 4.10 is the basis for the following result; recollect the definition of a super-uniform random quantity from Definition 4.7. This result is used in the proof of Theorem 4.6.
Theorem 4.11 If \(F\) is the distribution function of \(X\), then \(F(X)\) has a super-uniform distribution. If \(F\) is continuous then \(F(X)\) has a uniform distribution.
Proof: As we can see from Figure 4.1 \(F(F^-(u)) \geq u\) then, from Theorem 4.10, \[\begin{eqnarray*} \mathbb{P}(F(X) \leq u) & = &\mathbb{P}(F(F^-(U)) \leq u) \\ & \leq & \mathbb{P}(U \leq u) \\ & = & u . \end{eqnarray*}\] In the case where \(F\) is continuous, it is strictly increasing except on sets which have probability zero. Then \[\begin{eqnarray*} \mathbb{P}( F(X) \leq u) \ = \ \mathbb{P}( F(F^-(U)) \leq u) \ = \ \mathbb{P}(U \leq u) \ = \ u, \end{eqnarray*}\] as required. \(\Box\)