Studying mathematics
Barriers and reasonable adjustments
Emma Cliffe
Plan
- The Equality Act 2010 (Guidance)
- Barriers to studying maths: What forms them?
- The hidden transition
- Not adjusting to increasing diversity
- Disjoint professional domains
- Making reasonable adjustments in maths
- Resources
- Questions and discussion
Equality Act 2010 (Guidance documents)
"A person has a disability [...] if he or she has a physical or mental impairment and the impairment has a substantial and long-term adverse effect on his or her ability to carry out normal day-to-day activities."
- Ensure disabled students are not unjustly disadvantaged or unfavourably treated due to their disability.
- In a proactive manner, make anticipatory reasonable adjustments to resolve barriers to access.
- In addition to anticipating barriers staff should make reasonable additional adjustments if barriers remain.
This is a summary: you should read the full guidance yourself and also take heed of advice provided by your institution
Example anticipatory adjustment
"A university recognises that making an adjustment to provide handouts in advance in electronic format is a common anticipatory need for disabled students, for example students who lip-read, students with dyslexia and students with visual impairments. The university makes this adjustment and agrees timescales to ensure all staff have teaching notes available in this way. This is an example of an anticipatory adjustment."
Example additional adjustment
"It may be appropriate for a university to install a hearing loop in all its lecture theatres to anticipate deaf students’ needs, but it may not be reasonable for it to have a British Sign Language (BSL) interpreter on its payroll prior to any deaf students being admitted to the university."
Barriers to studying maths

What forms them?
Barriers to studying maths
- The hidden transition to university mathematics
- Do we provide disabled students with adequate information to enable them to prepare?
- Not adjusting to increasing diversity
- Are the learning and teaching environments we construct becoming more inclusive?
- Disjoint professional domains
- Are we working together to provide appropriate tools and support for mathematical modes of communication?
The hidden transition
Maths at university
"Generally, students are surprised by both the teaching method at university and the nature of university mathematics"
Thomlinson, Challis, and Robinson. 2009. Student Experiences of the Transition to University. MSOR Connections 9 (2): 48–51.
| School | University |
|---|---|
| Characterised by learning of processes through 'doing'; mastery in class possible | Characterised by learning of concepts; mastery in class unusual |
| Directed learning; repetitive practise; regular feedback | Independent learning; explorative practise |
| Can clarify in 'real time' | Often can't clarify in class |
| Regular experience of 'success'; right or wrong | Progress hard to 'see'; less deterministic |
| Maths resources provided in required formats | Expected to access maths resources independently |
| Specialist support near level of mathematical fluency | Specialist support with maths background rare |
The hidden transition
Mathematics at university level is
- "characterised by the need for a high degree of conceptual and abstract thinking within the learning process"
We need students to have the processing capacity to engage with concepts and abstract thinking.
- Students with a print disability, with difficulties with taking notes, memory and concentration may spend substantial processing capacity on entirely different tasks.
The hidden transition
- Applicants may make assumptions about the university mathematics learning environment, the skills required and strategies which might be appropriate
- The study skills, compensatory strategies, assistive technology and methods of working with human support a student may have used to be successful in school mathematics do not necessarily scale or carry over the hidden transition. They may become ineffective with no warning.
Do we provide disabled students with adequate information to enable them to prepare?
Quotes from Mathematics Subject Benchmark (Quality Assurance Agency for HE (2015))
Not adjusting to the increasing diversity
"The number of UK-domiciled entrants to full-time first degree courses with a known disability was 40,500 in 2014-15, which was an increase of 42 per cent since 2010-11." (HEFCE)
Neurodiversity...
is present when an exceptional degree of variation between neurocognitive processes results in noticeable and unexpected weaknesses in the performance of some everyday tasks when compared with much higher performances on a subset of measures of verbal and/or visual abilities for a given individual. These [...] include tasks of learning and remembering, time management, social interaction and attention span, as well as tasks requiring fine and gross motor movements
is a positive statement of differentiation
Grant, 2009. The psychological assessment of neurodiversity. Neurodiversity in higher education: Positive responses to specific learning differences, 33-62.
Dyslexia
Dyslexia mainly affects the development of literacy and language related skills. It is characterised by difficulties with:
- Phonological processing
- Rapid naming
- Working memory
- Speed of visual processing
This can result in difficulties with reading, writing, spelling, sequencing and memory. Areas of relative strength might include, for example, verbal comprehension, visual reasoning, and holistic, rather than sequential, processing.
Areas of difficulty in mathematics
- Notes/solutions may contain copying errors, symbol confusion/reversals, word substitution or be incomplete
- Reading errors. Working memory may be overloaded when processing conceptually abstract or multi-step material
- Layout, font and style of "traditional" mathematics texts can add to processing difficulties
- Difficulty forming and retrieving association between mathematical vocabulary, notation and concept
- Difficulty learning, or producing from understanding, accurately stated definitions, theorems and formulae
- Combining multiple aspects and sequencing in procedures, arguments or proofs can be challenging
- May have difficulties moving from concrete to abstract
Dyspraxia
Dyspraxia affects the planning of what you do and how you do it. It is associated with problems of perception, language and thought and is characterised by difficulties with:
- Motor coordination, including handwriting, drawing etc.
- Speed of visual processing
- Visual reasoning
- Working memory
This can result in difficulties with organisation, attention, spatial awareness, managing time and space, sequencing, memory and written expression. Areas of relative strength might include, for instance, verbal comprehension, verbal reasoning and 'out of the box' thinking.
Areas of difficulty in mathematics
- May have similar difficulties with processing speed and working memory as experienced by students with dyslexia but reading/spelling not specifically weak
- Spatial issues and weaker visual reasoning can have specific impacts e.g. geometry, concrete questions in 2D or 3D, seeing symmetry and structure
- Notetaking/solutions may be very difficult to read back, inaccurate and incomplete
- Drawings of figures etc. may be hard to follow
- May produce non-standard solutions
Asperger's syndrome
Asperger's syndrome is a form of autism. It is characterised by difficulties with:
- communication
- flexibility of thought
- the social environment
- sensory stimuli
This can result in difficulties with processing information, change, seeing another's point of view, concentration in presence of sensory stimuli and communication with peers. Areas of relative strength might include, for instance, a high level of focus on mathematics of interest, logical thinking, appreciation for detail and complexity of arguments.
Example difficulties
- Concentration and focus in lecture and other busy learning environments
- Processing information, deciding on what is important, notetaking and summarising
- Adapting to a new way of learning mathematics, flexibly transferring mathematical knowledge
- Seeing connections and the 'big picture'
- Group work - formal or informal - so may also believe they are the only one having difficulty in transition
- Adapting to less deterministic outcomes - e.g. that answer may no longer be simply right or wrong
- Motivation in areas of mathematics which are not of personal interest
Mental health issues and other conditions
Students with mental health issues, conditions which cause pain, fatigue or restricted movement and students with sensory impairments may experience difficulties with:
- With concentration, memory, motivation and organisation
- Reading standard print effectively, following real time exposition and taking notes simultaneously
- Using handwriting to take personal notes or to complete rough work
- Producing legible handwritten mathematics
- Using a standard computer or using their assistive technology to communicate mathematically and to access mathematical resources and software
Disjoint professional domains
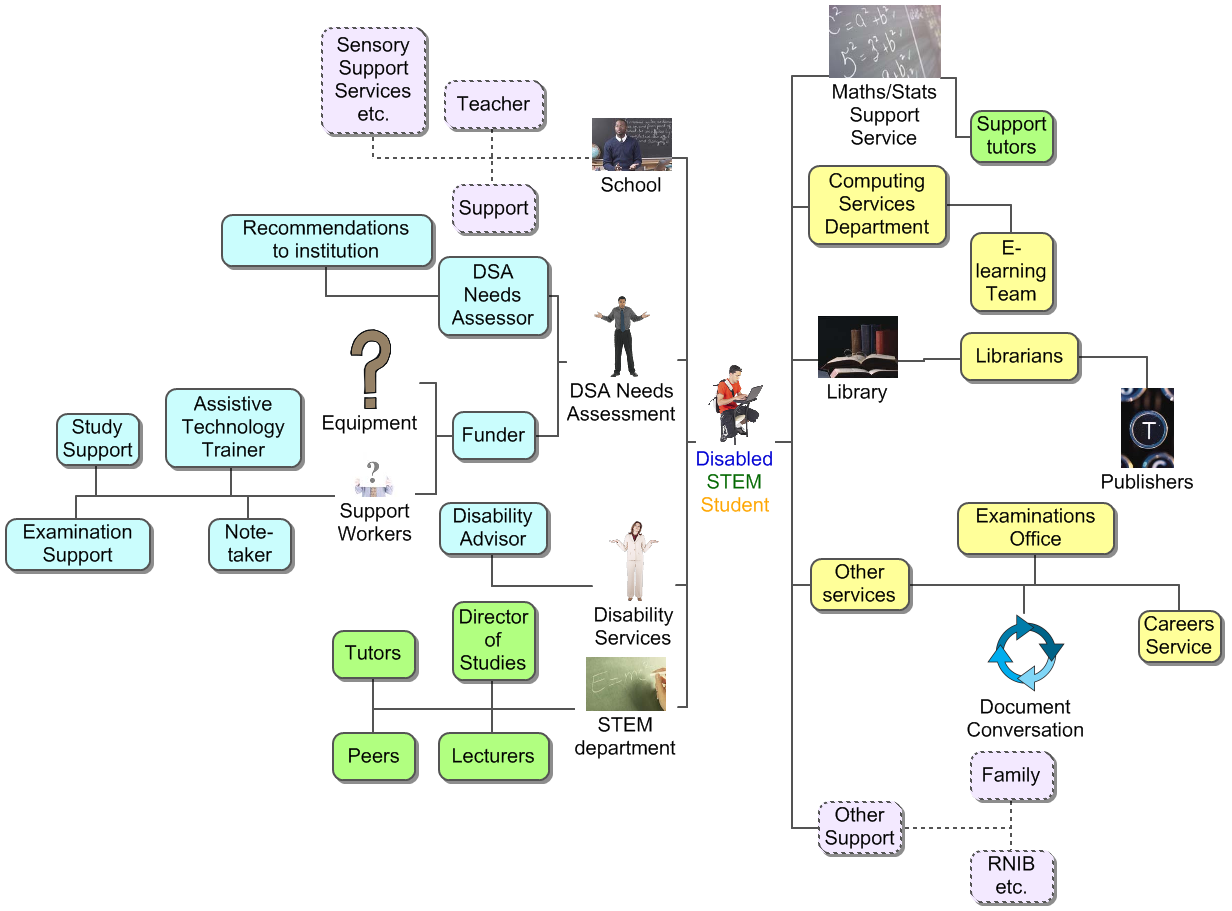
Assistive technology
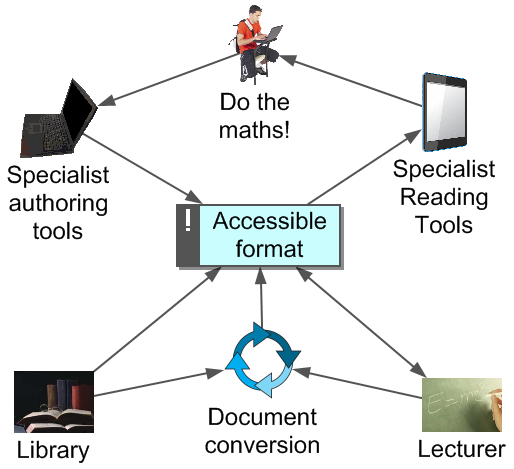
Mind the gap!
- Equations in PDF, print, PowerPoint, handwriting and many E-books are inaccessible to assistive technology. Word and HTML based formats are accessible to some assistive technology
- Using a computer and/or assistive technology to do and write up mathematics are specialist skills
- Nearly all of the software commonly provided by the Disabled Students Allowance process cannot be used effectively in mathematical learning environments...
SpLD support
This one to one support addresses the issues which some students might have in acquiring, recalling and retaining information in written and spoken language as well as the range of memory, organisational, attention and numeracy difficulties that students with specific learning differences often face when working in an HE context.
[...] This support should aim to develop students’ skills for autonomy in the learning environment. It should be tailored to a student’s individual needs [...]
Student Finance England, Non-Medical Help Services Reference Manual
Mind the gap!
A student may not build effective and appropriate mathematics study skills for their degree.
Without which effectively acquiring mathematical information and skills independently is difficult.
Constant fire-fighting erodes confidence...
and may challenge a core identity of maths students who "hated English but was good at maths".
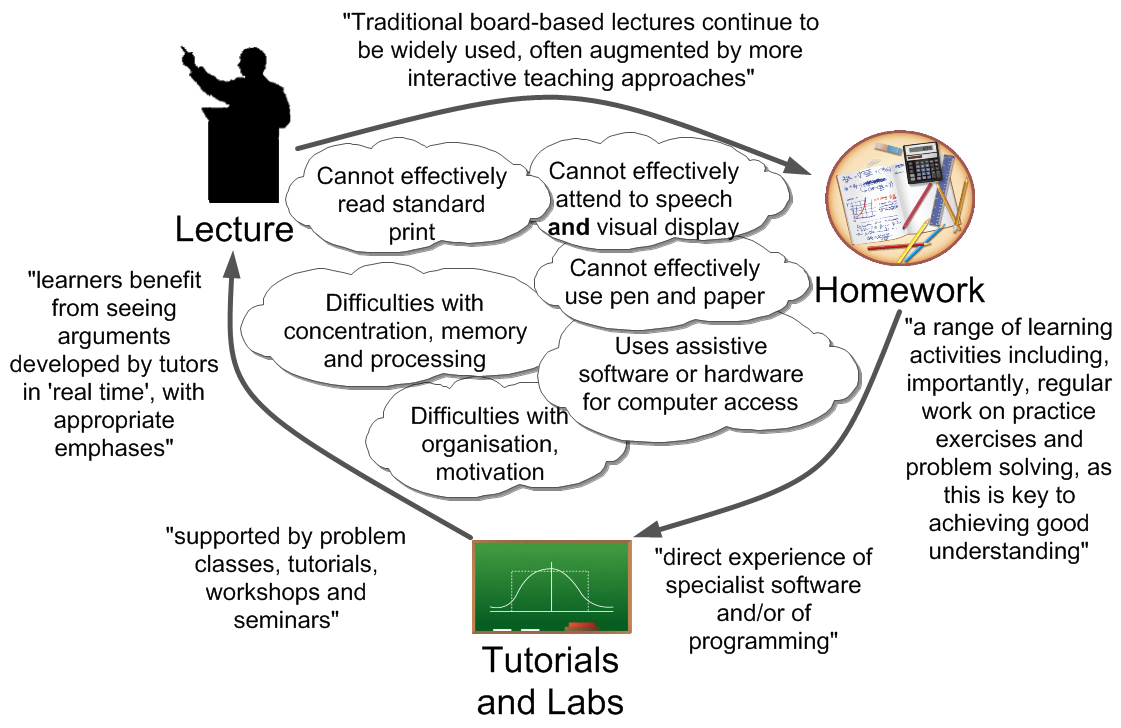
Making reasonable adjustments
in maths
Provide full notes prior to lectures
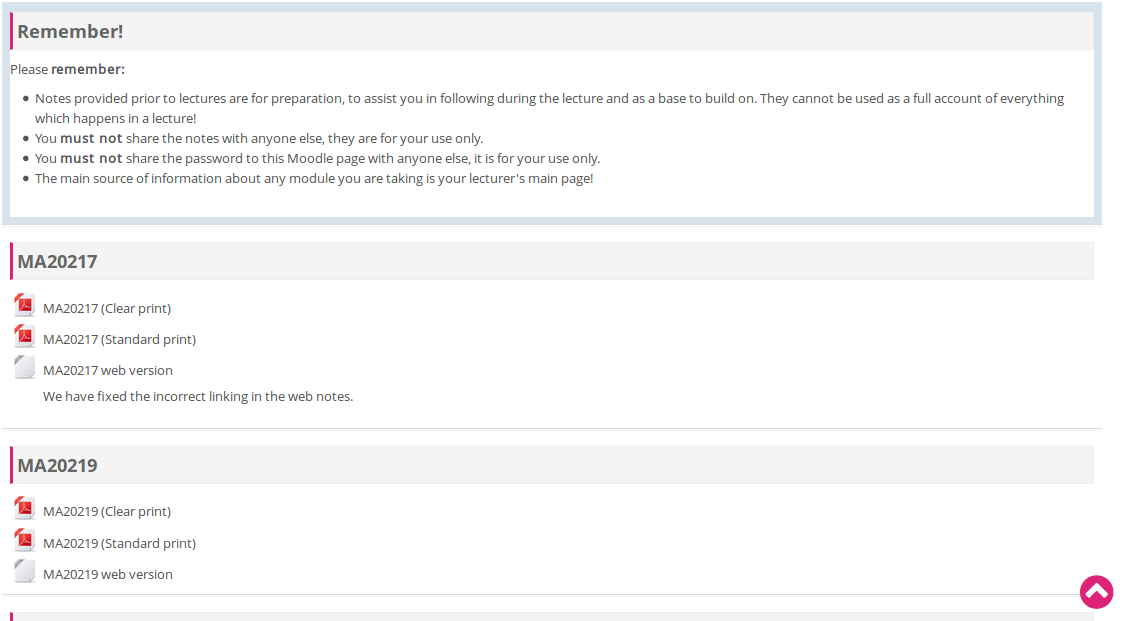
In suitable formats? The last 12 years
Quality Assurance Agency for HE (2015)
Learners benefit from seeing arguments developed [...] in 'real time' [...] Traditional board-based lectures continue to be widely used, often augmented by more interactive teaching approaches.
Equality and Human Rights commission (2011)
A common anticipatory adjustment of providing resources in advance in electronic formats.
What we want...
For all students to follow the lecture and to engage with the concepts and arguments!
We don't want other tasks e.g. careful copying to take precedence.
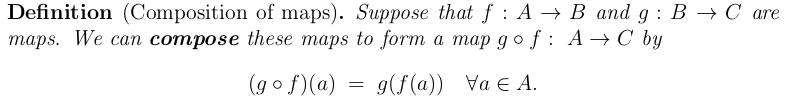
- "[I am] struggling to make accurate notes during the lecture."
- "Without the lecture notes there is no point in being there"
- "The notes our lecturer uploads [...] are in hand-written format which I find extremely difficult to read"
- "notes in text [...] would significantly facilitate my learning"
- "My eyes don't especially like the font and it is all a bit close together."
- "I often find my eye wanders around the page with some of the fonts that are used making it really difficult to follow what is being said/asked"
- "I wondered if I could get some editable ones as theres lots of gaps and font size changes on the PDFs online which make it really hard when I'm trying to read them."
- "Speech doesn’t work..."
- 2005/6: A blind student, specially produced notes
- 2006/7: Partially sighted student, specially produced notes; other disabled students offered these notes
- 2007-present: Only one academic year in which we had no maths student with visual impairment
- 2007/8: Student offers LaTeX; secure web delivery
- 2009/10: Admin support starts
- 2010/11: Interpretation of "anticipatory measures"
- 2011/12: HESTEM funding; produced a single master format and fragile conversions
- 2012: Student declares visual impairment during term 1
- 2015/16: Substantial changes to technology; produced single master more robust to conversion
- 2016/17: Supported academics who wished to in updating single master; conversions available on a central server
Who gets the notes?

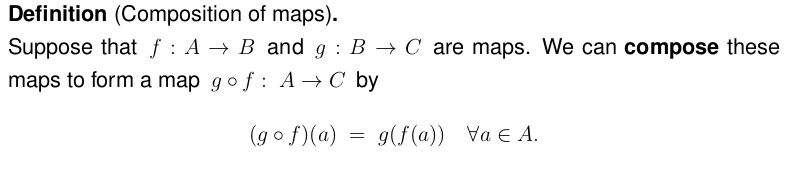
- "The combination of notes I have prior to lectures and the narrative that lecturer add, enables me to determine words and equations written on the board."
- "I have been finding them [clear print notes] much easier to read compared to other resources from lecturers"
- "My plan is to print the [clear print] PDFs into OneNote which should enable me to annotate them during lectures"
- "[It helps to] have notes and handouts laid out electronically, well-spaced out and so I can search within them using my computer"
- "The clear print notes are incredibly useful."
- "I would just like to say thank you. This service has been a great help over the last few years. Thank you very much for organising it and for providing quick help when it was needed."
We can also help staff out...
"in the case of [course materials the university] shall retain the right at any time to use, reproduce and adapt such materials freely for legitimate purposes."
2005-2017: We produced, preserved, maintained, updated, fixed and recovered LaTeX, returning it to staff as needed.
The future? Our main LaTeXer says "establishing a common standard for producing notes is the best way to not only produce accessible notes but to ensure easy transition between lecturers for a course"
- "Currently we don't have a set of typed lecture notes. I was wondering if by any chance you had a large printed version of notes from previous years and if I could use the tex-file. It would save me an enormous amount of time"
- "Here is the latex file for the notes, which [...] I am not able to compile" ... "Thank you - I was able to compile them!"
- "This is tremendously helpful and saves me hours of work."
- "If you have the LaTeX versions and would be able to send them to me that would be very helpful"
- "We recovered the source via optical character recognition and human checking and correcting for a student last year and I attach this." ... "Many, many thanks"
- "I am colour-blind [so] am unable to read [it]" ... "That's really helpful. I'd assumed there was nothing I could do about it."
Enable access to mathematical study skills
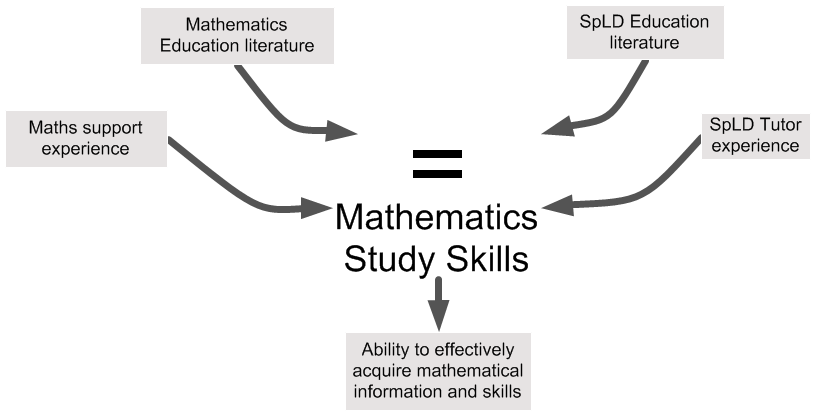


What might this include?
- Notetaking for mathematics, structured annotation
- Using expanding symbol range and vocabulary
- Building rich accurate concept images, example use
- Connecting and mapping concepts, visualisation
- Active reading for mathematics, self-explanation
- Problem classification, structured problem solving
- Developing an internal monitor, raising metacognition
- Approaches for learning processes and algorithms, using diagrams, overlearning, achieving automaticity
- Approaches for learning concepts, producing proofs, from concept image/map to 'reproduction', memory and maths
- Mathematical writing skills, as appropriate to level...
Where next?
- Embedding of skills use into first year problem sheets
- Self access short course on mathematical study skills
- Supported access long course
- Variant of course materials designed for use with general study skills tutors (constrained mathematical area) currently for DSA funded students only, students encouraged to follow up on using strategies in general mathematics support dropins.
- Referral to Mathematics Resource Centre group support if required. Students in these groups can access a limited amount of 1:1 support.
- Specialist 1:1 mathematics study skills tutorials (currently DSA funded only)
Take steps toward inclusive practice

Through project work and the mathematics specific literature
HEA Fellowship
"Fellowship of the Higher Education Academy is awarded to professionals who can demonstrate they meet the criteria of Descriptor 2 (D2) of the UK Professional Standards Framework (UKPSF) for teaching and supporting learning in higher education."
- Area of activity 4: Develop effective learning environments and approaches to student support and guidance
- Area of activity 5: Engage in [...] the evaluation of professional practices
- Professional value 1: Respect individual learners and diverse learning communities
- Professional value 2: Promote participation in higher education and equality of opportunity for learners
Engaging with the maths specific literature
There is a substantial body of literature on barriers and enablers for disabled students in mathematical subjects and on mathematical pedagogy more generally.
I have included a list which could serve as starting points for those exploring their own practice.
This might range from considering a simple 'checklist' for enabling neurodiverse students to engaging with the full literature on concept images or on enabling maths students who use assistive technology.
Use project work to explore change
Through Teaching Development Fund and the Reasonable Adjustments Project staff have access to funding to support exploration and change. Current projects:
- Pre-recording maths solutions to enable the syncing of handwriting of solutions with audio explanations to mirror real-time solutions classes as closely as possible.
- Delivery of 'flipped' classes where the learning is tailored and prioritised depending on the learning needs of the students.
- Using live streaming and short video tutorials to enhance and extend mathematics support.
Create a non-empty intersection!
Through the 12 years we also built experience and knowledge in the range of technical solutions and teaching and learning approaches which do work in a mathematical context.
Is it part of someone's job to:
- Support students in explaining areas of difficulty across the mathematical divide, providing context for both mathematics staff and those in professional services and to collaborate with all parties to reach solutions?
- Advise staff from disjoint professional domains on accessible teaching and learning in a maths context and to facilitate explanations, provide context and collaborate in change if required?
- Know about technology for mathematics access, to inform and support students or staff in using it and to collaborate with Computing Services, E-learning and the Assistive Technologists?
Resources
Current projects
- sigma Accessibility Special Interest Group (SIG): Join the mailing list, get involved... http://www.sigma-network.ac.uk/sigs/accessibility-sig
- STEM Enable: Crowdsourcing for locating and sharing information to enable disabled students studying STEM subjects, http://stemenable.referata.com
Starting points
Adams, Thomasenia Lott. 2003. Reading Mathematics: More than Words Can Say. The Reading Teacher 56 (8): 786–95.
Alcock, Lara. 2013. How to study for a mathematics degree. Oxford University Press.
Alcock, Lara, Mark Hodds, and Matthew Inglis. 2014. Self-Explanation Training for Mathematics Students. Mathematics Education Centre, Loughborough University.
Anthony, Glenda. 2015. When Mathematics Students Fail to Use Appropriate Learning Strategies. Mathematics Education Research Journal 8 (1): 23–37.
Brinkmann, Astrid. 2003. Graphical Knowledge Display - Mind Mapping and Concept Mapping as Efficient Tools in Mathematics Education. Mathematics Education Review, The Journal of Association of Mathematics Education Teachers 16: 39–48.
Chinn, S. J, and J. R Ashcroft. 2007. Mathematics for Dyslexics: Including Dyscalculia. 3rd ed. Whurr.
Cliffe, E. and N. A. Bradshaw. 2012. Autism Spectrum Disorders and Group Work in Mathematics. In Student-centred Approaches in Mathematics. National HE STEM Programme: Mathematical Sciences HE Curriculum Innovation Project, pp. 45–47.
Cliffe, E. and Peter Rowlett. 2012. Good Practice on Inclusive Curricula in the Mathematical Sciences, National HE STEM Programme: Mathematical Sciences HE Curriculum Innovation Project.
Starting points
Cliffe, E. and Jane White. 2012. Methods to Produce Flexible and Accessible Learning Resources in Mathematics. In Student-centred Approaches in Mathematics. National HE STEM Programme: Mathematical Sciences HE Curriculum Innovation Project, pp. 35–43.
Felder, R.M. and L.K. Silverman, Learning and Teaching Styles in Engineering Education, Engr. Education, 78(7), 674-681 (1988 with 2002 preface).
Grove, Michael, Tony Croft, Joe Kyle, and Duncan Lawson. 2015. Transitions in Undergraduate Mathematics Education (includes: Trott, C. The neurodiverse mathematics student and Cliffe, E. Creating an accessible learning environment: Anticipating and resolving practical barriers). University of Birmingham.
Houston, Kevin. 2009. How to Think Like a Mathematician. Cambridge University Press.
Iannone, Paola and Adrian Simpson. 2012. Mapping University Mathematics Assessment Practices. University of East Anglia.
Institute of Physics. 2017. Building momentum towards inclusive teaching and learning: A good-practice guide for undergraduate physics.
Institute of Physics. 2013. Supporting STEM students with dyslexia: A good practice guide for academic staff.
Starting points
Mason, John, Leone Burton, and Kaye Stacey. 2010. Thinking Mathematically. 2nd ed. Pearson Education Limited.
Polya, G. 2014. How to Solve It: A New Aspect of Mathematical Method. Princeton University Press.
Portland Community College, 2013. Making Math More Accessibility at PCC.
Schoenfeld, Alan H. 1992. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334-370). New York: MacMillan.
Shepherd, Mary D., and Carla C. van de Sande. 2014. Reading Mathematics for understanding - From Novice to Expert. The Journal of Mathematical Behavior 35 (September): 74–86.
Tall, David, and Shlomo Vinner. 1981. Concept Image and Concept Definition in Mathematics with Particular Reference to Limits and Continuity. Educational Studies in Mathematics 12 (2): 151–69.
Velleman, Daniel J. 2006. How to prove it: A structured approach. Cambridge University Press.
Vivaldi, Franco. 2014. Mathematical writing. Springer.
Williams, Carol G. 1998. Using Concept Maps to Assess Conceptual Knowledge of Function. Journal for Research in Mathematics Education 29 (4): 414–21.
Questions and discussion
These slides are available at:
http://people.bath.ac.uk/cspehj/slides/MathsBarriersAdjust/
My email address is:
E.H.Cliffe@bath.ac.uk

