|
Longitudinal MOKE
In the longitudinal case,
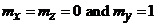 . Eq. 11.5 then becomes:
|
 |
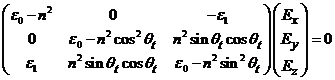(Eq.12.1) |
This leads to:
|
 |
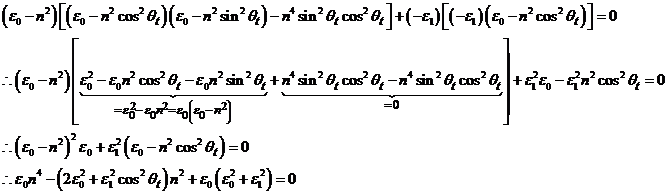(Eq.12.2) |
And we recognize a second order equation with solutions:
|
 |
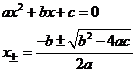(Eq.12.3) |
Therefore, we can write:
|
 |
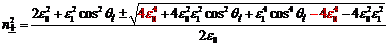(Eq.12.4) |
If we then keep only terms that are linear in
ε1,
|
 |
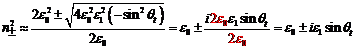(Eq.12.5) |
These are the eigenvalues for the wave equation, corresponding to the
eigenvectors:
|
 |
(Eq.12.6) |
where we recognize the expressions for left and right circularly polarized
light waves.
© V. K. Valev
|