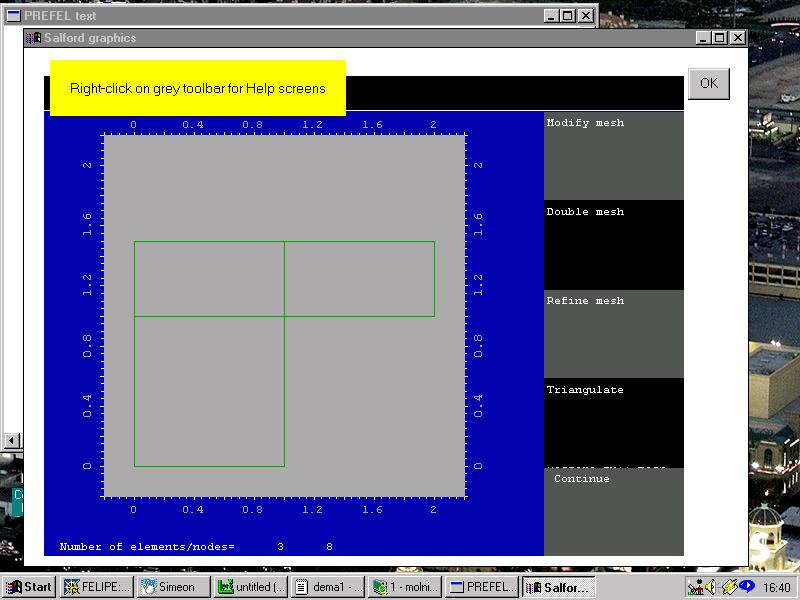

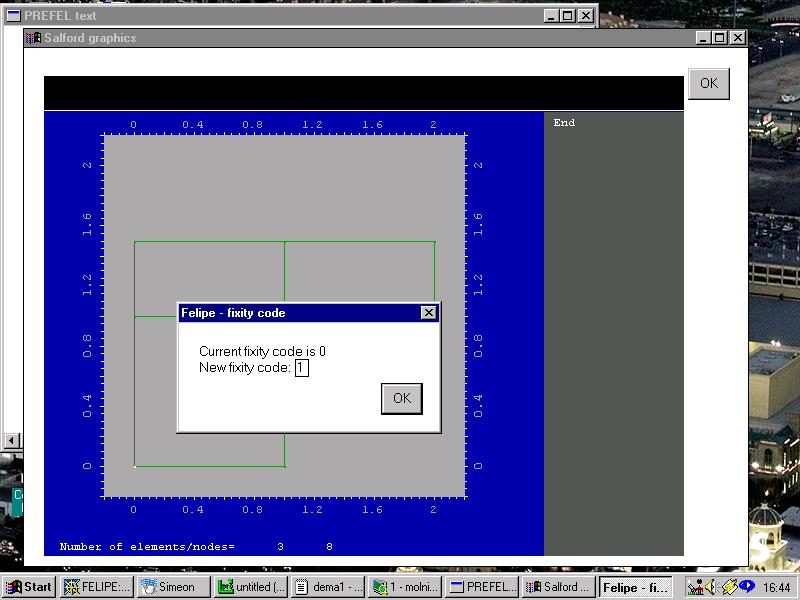
In the picture below, the Dirichlet condition has been applied; this is indicated by the left-hand edge of
the region being drawn in grey.
The next step is to refine the mesh, by clicking on "Refine" on the menu bar...
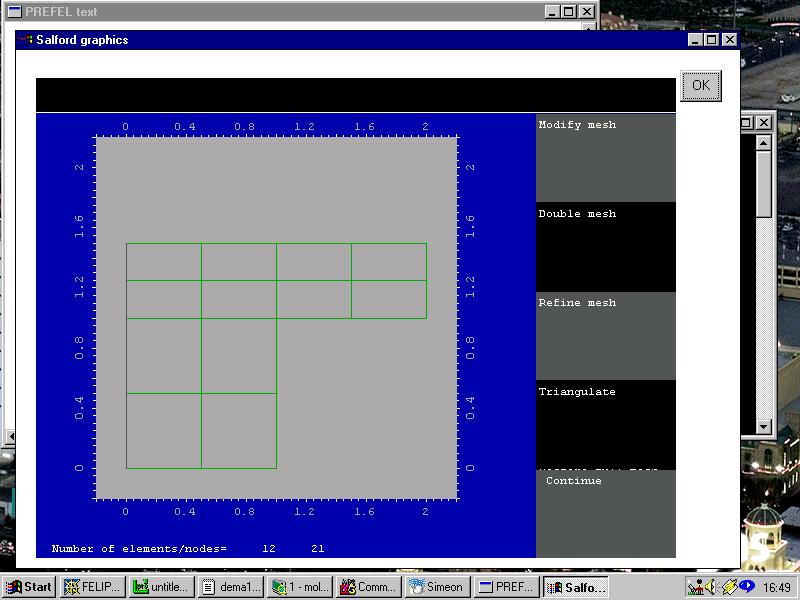
In the next picture, the mesh has been refined by subdividing each quadrilateral element into four; this operation can be carried out automatically, with a single click of the mouse! (Manual refinement of particular regions is also possible, as shown in the elasticity example later).
In order to produce the H-shaped region needed, we now select "Double mesh" from the menu bar. A mesh can be "doubled" either by translation or by reflection, in any one of the four cardinal directions. In the picture below it has already been doubled by reflection in the positive x direction (i.e. to the right), and is about to be doubled by reflection again in the positive y direction (upwards)...
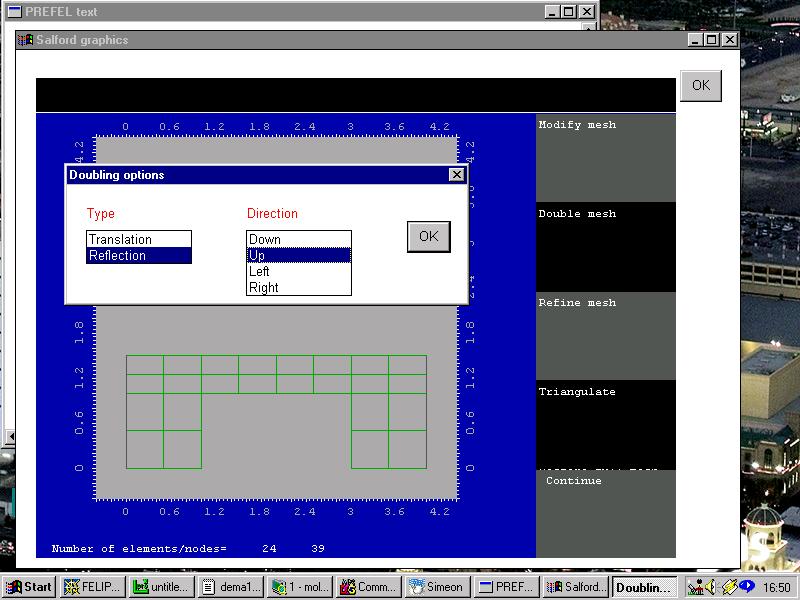
In the resulting mesh, note that the Dirichlet condition has been copied to both the left and
right-hand vertical edges.
The final step is to triangulate the mesh, as the "main engine" is written for linear triangle elements. Each quadrilateral element will be cut into two linear
triangles (Triangulation can also produce six-noded triangles from eight-noded quadrilaterals, even with curved sides!)...
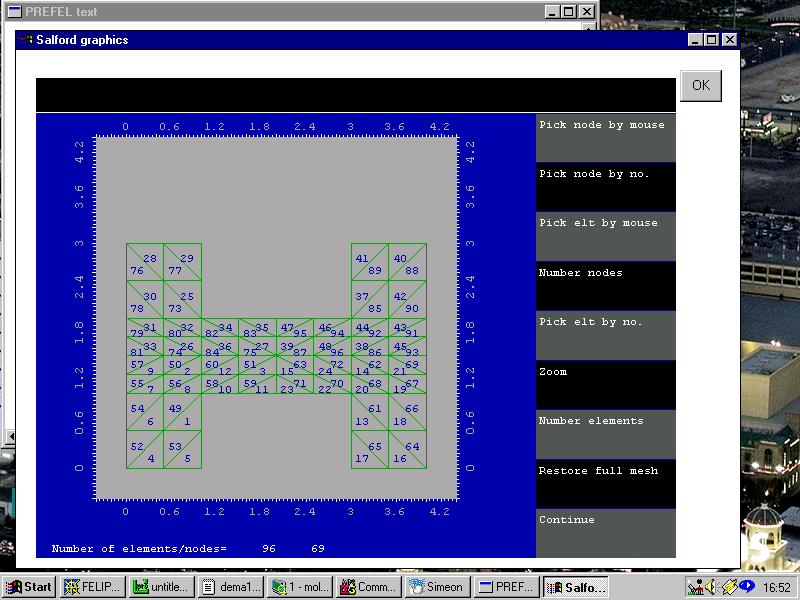
The final mesh, with element numbering added, is displayed below...