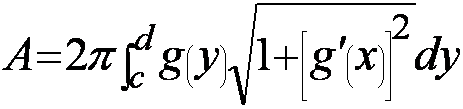MA10003

3.9 APPLICATIONS OF

INTEGRATION:

· Volumes of Revolution

· Length of a Plane Curve

· Area of a Surface of Revolution

I. Volumes of Revolution

A solid obtained by revolving a plane region about an axis of revolution lying in the same plane.

Method:

· Find the cross-sectional area at each point along axis

· Sum these areas to give volume.

Case 1:

Axis of revolution = x axis

(Volume by disks in Anton)

Case 2:

Axis of revolution = y axis

(Volume by disks in Anton)

Case 3:

Volume hollow in centre

(Volume by washers)

II. Length of a Plane Curve

If y=f(x) is a smooth curve (i.e. continuous) on interval [a, b], then arc length L is defined as

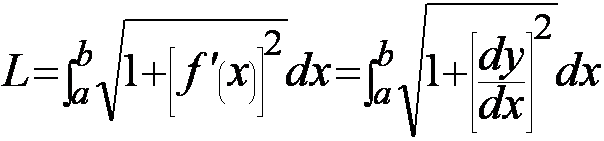
Similarly for curve x=g(y), smooth on interval [c,d], the arc length L is defined as

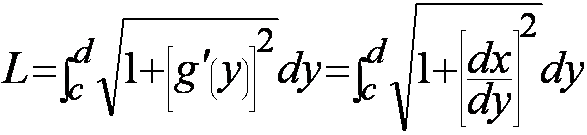
Note:

For curves in parametric form

x=x(t), y=y(t) for

if 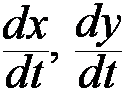are continuous

provided no segment of the curve is traced more than once as t increases

arc length L is

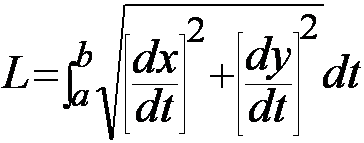
III. Area of a surface of revolution

If y=f(x) is rotated about the x axis on the interval [a, b], the area of surface of revolution between x=a and x=b is

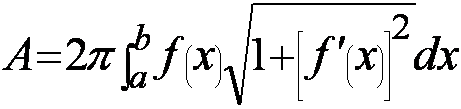
For curve x=g(y), rotated about y axis on interval [c, d], the area of surface of revolution between x=c and x=d is