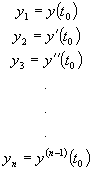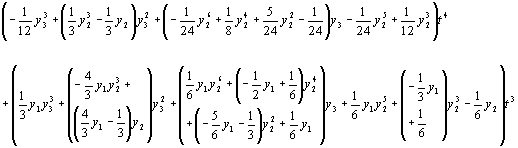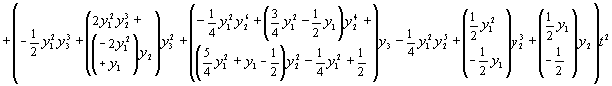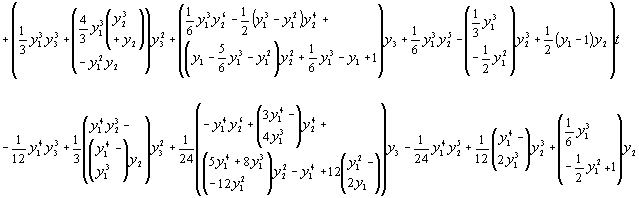Composite Computing Methods Integrating
Symbolic, Numeric and Graphical Packages for Research Engineers
Joint Technologies Applications
Project JTAP 5/11
Final Report
James H Davenport
Brian J Dupée*
Department of Mathematical
Sciences University of Bath
Claverton Down
Bath BA2 7AY United Kingdom
email:jhd,bjd@maths.bath.ac.uk
30 September 1999
* Dr Brian Dupée is now a Lecturer in the School
of Computing at Napier University, 219 Colinton Road,
Edinburgh EH14 1DJ. Email: brian@dcs.napier.ac.uk.
Contents
1. Introduction *
Project Outline *
Technology Issues *
2.  for
Windows *
for
Windows *
3. New Applications of Composite Algorithms *
Taylor Series Methods *
Introduction
*
Taylor
Series Methods *
Composite
Methods *
The
Integrated Algorithm *
Examples
*
Incorporation
into ANNA *
Graphical Features *
Interpolation Package *
Introduction
*
Interpolating
Functions *
The
Package *
The
Learning Package in Use *
Conclusions
and Further Work *
Example
Problem Sheet *
4. Dissemination *
5. Bibliography *
Introduction
Project
Outline
The project "Composite Computing Methods Integrating Symbolic, Numeric
and Graphical Packages for Research Engineers" was to build on the results
of the research undertaken for the JISC project "More Intelligent Delivery
of Numerical Analysis to a Wider Audience". In particular, it is to investigate
combining and extending the capabilities of the expert system  ,
developed under the previous project, with graphical packages for the display
of numerical and symbolic/numerical data, together with the implementation
of further algorithms and techniques using a combination of symbolic and
numerical methods.
,
developed under the previous project, with graphical packages for the display
of numerical and symbolic/numerical data, together with the implementation
of further algorithms and techniques using a combination of symbolic and
numerical methods.
Technology
Issues
The development of the Axiom Computer Algebra System, which underlies
this project, continues in the two directions as outlined in previous reports.
However, NAG have put a temporary hold on the introduction of version 2.2
for each of Windows and Unix systems which has affected our ability to
institute a comprehensive testing procedure for our proposed packages.
We have, however got ready for such, by upgrading the Sun workstation to
the Solaris operating system and the PC to Windows NT4 together with the
necessary memory upgrades.
The Unix version of Axiom will be supplied with  as an integral part. This version of
as an integral part. This version of  has thus been upgraded to include better explanation and automatic tuning
mechanisms and underwent considerable testing as required by NAG.
has thus been upgraded to include better explanation and automatic tuning
mechanisms and underwent considerable testing as required by NAG.
-
 for Windows
for Windows
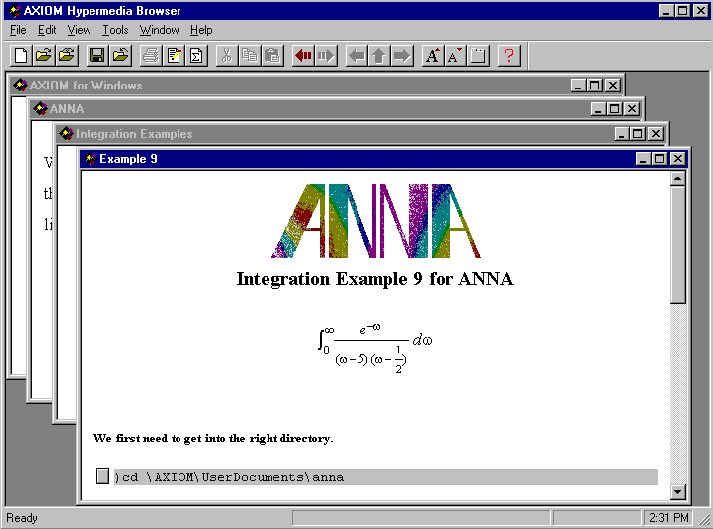
Figure 1:  for Windows Integration Example
for Windows Integration Example
Recently, the development of Axiom to use Windows technology on PC's
(Versions of Axiom for Windows exist currently for Windows 95 and Windows
NT 4) has further augmented its graphical possibilities which, together
with much greater use of high quality Hypertext Graphical User Interface,
using IBM's Techexplorer, allows the instigation of research programmes
into the exploitation of these links between the various technologies.
It is envisaged that these improvements will eventually be transferred
to systems on other platforms.
To date, NAG have introduced the ability to call a number of Fortran
Library routines to the Windows version of Axiom. These include most of
the Integration chapter of the Foundation Library and a number of Eigenfunction
and Special Functions. This means that it is thus possible to implement
the Integration chapter of  on the PC.
on the PC.
The technology for implementing ASP's and other Fortran related issues
has been altered and/or rationalised such that direct transfer of programs
written for the Unix versions of Axiom will not work. However the alteration
of much of the code for use under Windows is time-consuming, but not arduous.
This rationalisation is likely to be required eventually for all versions
and so is a useful exercise.
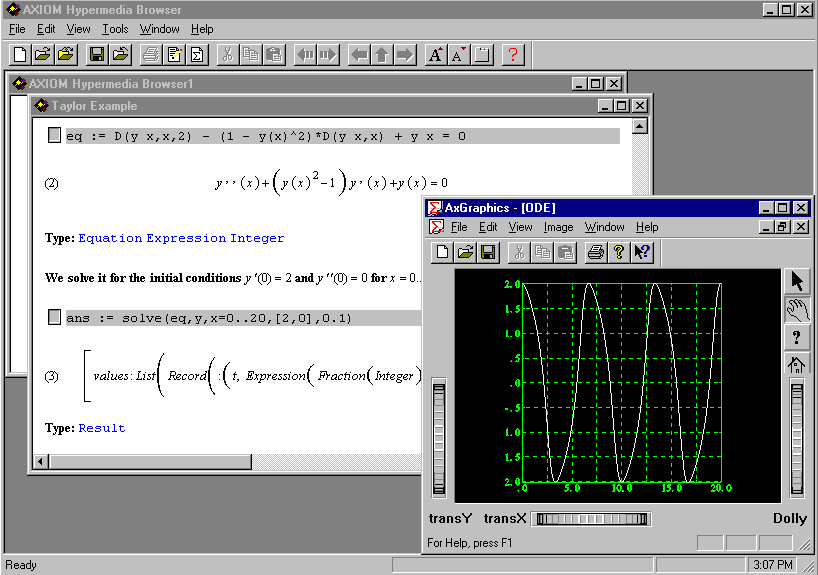
Figure 2:  for Windows Taylor Series Methods Example
for Windows Taylor Series Methods Example
To this end, we have implemented a working version of most of the Integration
chapter of  on the PC. This
has been tested in Bath and at the Universidad Polytécnica de Madrid.
Since the system uses much altered technology and increased graphical display
and formatting possibilities, I have provided it with a range of graphical
interfaces, thus allowing us some idea of the uses to which we could put
the new system.
on the PC. This
has been tested in Bath and at the Universidad Polytécnica de Madrid.
Since the system uses much altered technology and increased graphical display
and formatting possibilities, I have provided it with a range of graphical
interfaces, thus allowing us some idea of the uses to which we could put
the new system.
-
New
Applications of Composite Algorithms
Work has continued in the area of a new numeric/symbolic algorithm using
Taylor Series methods for the numerical solution of initial value problems
of ordinary differential equations [Dupée & Davenport, 1999].
This has led to an algorithm for the solution of such a problem (and its
display) that has been implemented and undergone considerable testing.
It has also been integrated into the structure of  and will be made available in two modes --- either as a stand-alone method
for use directly with Axiom or within the upgraded
and will be made available in two modes --- either as a stand-alone method
for use directly with Axiom or within the upgraded  .
.
The collaborative work with the Escuela Técnica Superior de Ingenieros
Industriales of the Universidad Politécnica de Madrid on the implementation
of a teaching package combining Numerical, Symbolic and Graphical packages
for the calculation and display of comparative methods of interpolation
is close to completion. It has also undergone considerable testing and
will be made available shortly as a separate package.
Taylor
Series Methods
One of the basic techniques in every mathematician's toolkit is the
Taylor series representation of functions. It is of such fundamental importance
and it is so well understood that its use is often a first choice in numerical
analysis. This faith has not, unfortunately, been transferred to the design
of computer algorithms.
Approximation by use of Taylor series methods is inherently partly a
symbolic process and partly numeric. This aspect has often, with reason,
been regarded as a major hindrance in algorithm design. Whilst attempts
have been made in the past to build a consistent set of programs for the
symbolic and numeric paradigms, these have been necessarily multi-stage
processes. Using current technology it has at last become possible to integrate
these two concepts and build an automatic adaptive symbolic-numeric algorithm
within a uniform framework that can hide the internal workings behind a
modern interface.
Introduction
This section introduces a symbolic-numeric implementation of Taylor
Series methods for the solution of initial value ODE problems. Hitherto,
the only implementations have been wholly numeric, wholly symbolic or obviously
a multi-stage process (one where the symbolic and numeric calculations
are carried out separately with at least one other stage between them).
Such methods present a variety of computational problems, some of which
are better solved symbolically, others numerically. This section identifies
the characteristics of such methods and presents an algorithm for better
evaluation.
The techniques of approximating an ODE by a Taylor Series has been known
for many years and has been implemented, for example, by a group led by
A. C. Norman in Cambridge, UK, in the package 'TAYLOR' [Norman, 1973; Norman,
1975; Norman, 1976; Barton et al., 1971a] using the analysis by Barton,
Willers and Zahar [Barton et al., 1971b]. An alternative package, 'ATSMCC'
(Automatic Taylor Series by Morris, Chang and Corliss) [Corliss & Chang,
1982], was also made available a few years later. In operation, these packages
generate appropriate Fortran code to define the Taylor series and the evaluation
process, given the ODE and initial conditions, for further compilation
and operation. So they are at least a three-stage process. In [Corliss
& Chang, 1982], Corliss and Chang freely admit that:
"When all the computer time for preprocessing, compiling,
linking and execution was included, the relatively high system-dependent
cost of linking with the library routines overwhelmed most other differences
in CPU times."
The user-time performing the intervening stages (compilation, linking etc.)
only added to the overall cost.
Some Computer Algebra Systems (CASs), such as Maple [Heck, 1996], Axiom
[Jenks & Sutor, 1992] and Mathematica [Wolfram, 1996], have the necessary
algorithms built-in to calculate the Taylor series symbolically. After
all, this is a purely symbolic process. The evaluation stage is performed
separately, usually symbolically even though this is computationally expensive.
The implementation in this project, written for the CAS Axiom, is a
single composite process which takes the ODE and initial conditions, creates
the Taylor series, automatically generates the Fortran evaluation code
which it then compiles, links and runs before returning the required result.
The trade-off for the speed of the evaluation process using Fortran
is in the cost of the Fortran generation and compilation(The Fortran generation
process in Axiom is the costliest in practice although the compilation
itself is at least of the order n*n on the size of the code). It therefore
makes sense to limit the size of the generated Fortran code as much as
is reasonable. The speed-up over purely symbolic code is thus optimised.
The better ease of use when compared to the purely numerical methods and
applications like 'TAYLOR' and 'ATSMCC' is self-evident.
The section includes comparisons between the new implementation, Taylor
series methods using purely symbolic code and using alternative symbolic-numeric
code.
Taylor
Series Methods
The two papers by Barton, Willers and Zahar [Barton et al., 1971a; Barton
et al., 1971b] provide a complete description and analysis of the method.
However, we will give a summary.
The method is described in [Barton et al., 1971b] as an application
of the process of analytic continuation. So, given a system of Differential
Equations:
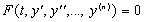 (1)
linear in
(1)
linear in 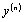 and initial conditions
and initial conditions
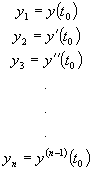
all specified, the Taylor series expansion about  for
for 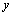 is given as
is given as
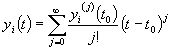 (2)
The general idea is that this, or rather its approximation
(2)
The general idea is that this, or rather its approximation
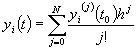 (2’)
is evaluated at
(2’)
is evaluated at 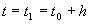 , the series
is then expanded about this point and the process continued. The calculation
of the Taylor series expansion is described in [Barton et al., 1971a].
, the series
is then expanded about this point and the process continued. The calculation
of the Taylor series expansion is described in [Barton et al., 1971a].
The analysis of the method in [Barton et al., 1971b] shows that the
method is extremely accurate and that, given a step-length 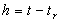 ,
the local error
,
the local error 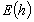 will be
small if
will be
small if
-
the error involved in the truncation of the Taylor series is at least as
small as the tolerance
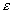
and
-
the step-length chosen minimises
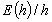
.
The ideal truncation 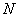 is assumed to be the equal to the number of significant digits of the platform
and is found to be only slightly dependent on the tolerance. However, since
is assumed to be the equal to the number of significant digits of the platform
and is found to be only slightly dependent on the tolerance. However, since 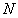 was not found to be particularly sensitive to the equations integrated,
this value must only be considered as an arbitrary ideal.
was not found to be particularly sensitive to the equations integrated,
this value must only be considered as an arbitrary ideal.
In the ‘TAYLOR’ package, given the example
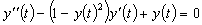 (3)
(van der Pol's equation with
(3)
(van der Pol's equation with 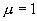 )
[Zwillinger, 1989] and initial values
)
[Zwillinger, 1989] and initial values
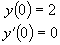
the Fortran code is generated using the commands (in a file)
INDEP T
DOUBLE
INIT SETUP
Y(0) = 2
Y'(0) = 0
EQNS
Y"=(1-Y**2)*Y' - Y
ADV VAL(Y,Y',T)
which will cause the program to create a number of Fortran subroutines
for describing and evaluating the Taylor series. The user must then create
a main program (in Fortran or C) to utilise these subroutines (enter parameters,
print results etc.), compile, link and run the binary.
The main differences in ‘ATSMCC’ is in the calculation of the truncation
value 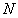 and the appropriate
step-size. Even though it requires less user control, the complete program
has, in general, five stages:
and the appropriate
step-size. Even though it requires less user control, the complete program
has, in general, five stages:
-
create and edit the input,
-
preprocess to translate the input into object code,
-
compile the Fortran object code,
-
link with the ATSMCC subroutine library, and
-
execute the resulting load module to solve the problem.
Some of these steps may be combined and others may only need to be performed
once if a single problem is to be solved repeatedly. However, this program
structure does not lend itself towards a flexible and natural user-friendly
interface.
The code supplied with some of the CASs use purely symbolic techniques.
The main problems occur during the evaluation process since the number
of substitutions (evaluations) of the parameters at each step is very large.
Since substitutions are time-consuming, this part of the process is very
inefficient. If the Taylor series evaluation process is compiled, there
is some improvement, but not sufficient to boost the efficiency enough
to be considered anything more than an exercise.
Composite
Methods
Symbolic-numeric methods as implemented, for example, in  [Dupée & Davenport, 1996] use symbolic analysis to identify
sufficient parameters to be able to select and implement numeric procedures,
usually from the NAG Fortran Library. The results are then returned for
further symbolic processing. Underlying this is the ability within Axiom
to create, compile and link Fortran evaluation procedures, named ASPs (Argument
Sub-Programs), at run-time [Broughan et al., 1991; Keady & Nolan, 1994].
[Dupée & Davenport, 1996] use symbolic analysis to identify
sufficient parameters to be able to select and implement numeric procedures,
usually from the NAG Fortran Library. The results are then returned for
further symbolic processing. Underlying this is the ability within Axiom
to create, compile and link Fortran evaluation procedures, named ASPs (Argument
Sub-Programs), at run-time [Broughan et al., 1991; Keady & Nolan, 1994].
The technology to perform such processes, Nagman and nagd,
is described in [Dewar, 1994]. In essence, the Nagman local agent
manages the data-transfer between the different computing protocols, using
RPC (remote procedure call) to pass the data to the NAG daemon (nagd),
which may be running on a remote system. The nagd incorporates a
main program (stub), the Fortran library routine with appropriate C header
files and the Axiom-generated ASP, performs the compilation and runs the
resulting binary. The results are fed back through the Nagman to
the current Axiom session.
The Fortran generation utilities included with recent implementations
of Axiom are used to both create the Fortran code and also to verify that
the full ANSI 1978 standards are adhered to with respect to variable names,
types and constructs. The verification is necessary since the code may
need to be compiled on a remote machine of indeterminate operating system
and with any compiler.
All pre- and post-processing are performed within Axiom packages or
the interactive session. The use of these packages, which may involve the
use of the Axiom Category and Domain structures, allows for the automation
of the complex processes and can thus become part of an intricate user
interface.
In this implementation, since we are generating the algorithm as
opposed to the sub-programs at runtime, the Fortran subroutine corresponding
to the algorithm has to be compiled (using the same Fortran compiler as
recognised by the nagd) and placed in a library to be accessed in
a similar way to the access of the NAG Fortran Library's algorithms. The
C header file is placed alongside the other C source files in the nagd
directory
structure and the Axiom code (the ASP Domain and the Taylor series method
Package) is compiled as usual.
| Algorithm 1: ODESolveTaylorSeries
%preprocessing
calculate N from size of system
%symbolic processing
compute formal (lazy) Taylor Series
truncate Taylor series to order N
% code-creation, compilation and linking
calculate workspace requirements
create ASP
initiate Nagman
compile Fortran code
run Fortran code
%post processing
return result
remove unwanted workspace
print result |
Figure 3: The New Algorithm
The
Integrated Algorithm
The Taylor series representation is calculated symbolically within the
Axiom Package ExpressionSpaceODESolver (written by Manuel Bronstein)
which returns a lazy Taylor series in 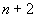 variables where
variables where 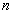 is the
order of the ODE. For this implementation this is truncated to form a polynomial
in
is the
order of the ODE. For this implementation this is truncated to form a polynomial
in 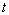 of order
of order 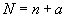 where
where 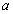 is an integer which
can be estimated in the pre-processing stage (depending on the required
accuracy and estimate of stiffness) and where the other variables may be
of arbitrary order. So, for example, Equation (3) could be approximated
by (in the case where
is an integer which
can be estimated in the pre-processing stage (depending on the required
accuracy and estimate of stiffness) and where the other variables may be
of arbitrary order. So, for example, Equation (3) could be approximated
by (in the case where 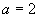 ):
):
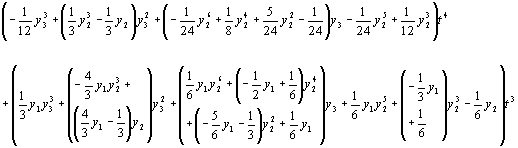
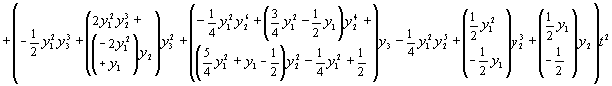
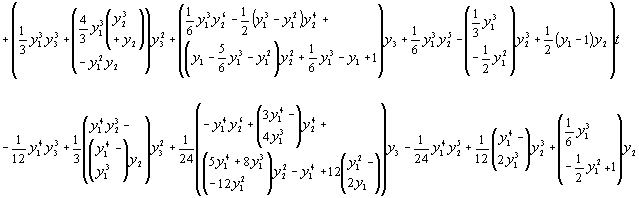
The calculation of the optimum value of the truncation parameter is
critical. This is since the prime costs in this algorithm are in the Fortran
generation, compilation and linking stages, as opposed to the evaluation
stages of a fully symbolic system or the purely numeric stages of 'TAYLOR'.
We can therefore consider, if necessary, using smaller step-sizes than
those recommended in [Barton et al., 1971b] rather than a larger polynomial
system to cut down this cost but we then leave ourselves open to problems
with any ODE showing more than the mildest of stiffness (since in a stiff
system, there will be more information contained in the coefficients of
the higher exponents of the Taylor series. An alternative Taylor series
algorithm for stiff equations is described in [Barton, 1980] but this is
much more expensive computationally and it is not apparent that there would
likely be any major cost or accuracy benefits over other stiff methods.).
We must, though, ensure that all appropriate 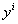 are calculated.
are calculated.
It must be noted that the step-sizes mentioned above are, or can be,
much larger than the step-sizes used in other ODE solvers such as Runge-Kutta.
The initial ‘test evaluation’ can use a step-size of as much as 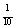 of
the complete range of integration. So the usual number of steps is often
much less than other methods.
of
the complete range of integration. So the usual number of steps is often
much less than other methods.
The polynomial is then coded into a Fortran ASP. Each monomial becomes
one line of Fortran code to better facilitate the calculation of the return
values 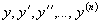 . This is then passed
to the nagd for compilation and linking. Whilst Horner's rule should
normally be preferred for evaluation, it is not, as yet, available in Axiom.
There are other considerations though. Since the most costly part of the
algorithm is in the ASP generation and not the evaluation, the use of Horner's
rule would not make a significant difference. Indeed, the size of the code
may
be larger and thus less efficient overall.
. This is then passed
to the nagd for compilation and linking. Whilst Horner's rule should
normally be preferred for evaluation, it is not, as yet, available in Axiom.
There are other considerations though. Since the most costly part of the
algorithm is in the ASP generation and not the evaluation, the use of Horner's
rule would not make a significant difference. Indeed, the size of the code
may
be larger and thus less efficient overall.
Other pre-processing stages include the estimation of the amount of
workspace required for the calculation stages and the setting up of the
appropriate matrices. For this, a reasonable estimate must be made of the
number of iterations that may be required in the calculation. This is not
an easy task since the algorithm is designed to be adaptive i.e. alter
the step-length according to the changes in the values of 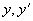 etc. Obviously a `quick and dirty' method of estimating the workspace requirements
may be inaccurate but sufficient. A reasonable overestimate is all that
is required. This is calculated as a function of the truncation parameter,
etc. Obviously a `quick and dirty' method of estimating the workspace requirements
may be inaccurate but sufficient. A reasonable overestimate is all that
is required. This is calculated as a function of the truncation parameter, 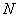 ,
the
,
the
order of the ODE, 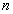 , and
the required tolerance.
, and
the required tolerance.
The Fortran library program, after checking input values for consistency,
calculates a weight function (a function of the input values) and evaluates
its first step. On the result of this evaluation it re-calculates the weight
function to get a good basic estimate for the step-size before recalculating
the first step. It then goes through the evaluation process modifying the
step-size as appropriate. All of the calculated values for 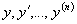 are returned.
are returned.
In order to present the information in as consistent a way as possible,
the post-processing stages remove some of the excess workspace and re-order
those that are left. It does, however, one other important job. If the
numerical process was unable to get a sufficient answer, it may re-calculate
the initial step-size or increase the amount of workspace before re-initiating
the calculation.
Examples
Example 1: Using the system, equation (3) is solved with the commands
(which can be entered directly using the command window or by completing
the HyperDoc forms):
(4) -> solve([Y[2],(1-Y[1]*Y[1])*Y[2]-Y[1]],0.0,20.0,[2.0,0.0],1.0e-4)
which calculates the values of 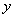 and
and 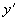 from
from 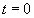 to
to 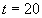 and gives the result
and gives the result
(4)
[ifail: Integer, intensityFunctions:
List(String), method: Result,
result: Matrix(DoubleFloat),
y: Matrix(DoubleFloat),
xout: Matrix(DoubleFloat), explanations:
List(String),
x: DoubleFloat, count: Integer]
Type: Result
(5) -> %.y
(5) [2.00912125487821
- 0.00769178896780431]
Type: Matrix DoubleFloat
in 207 iterations. The field y here contains
the values of 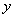 and
and 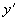 at the end point.
at the end point.
The returned fields in the result are:
ifail: The return status – a non-zero value indicates a failure
intensityFunctions: The attributes of the system of ODEs
as discovered by 
method: The method used for the calculation
explanations: The reasons for  ’s preference for the method used
’s preference for the method used
x: The last calculated point
y: The values of 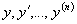 at
the end point
at
the end point
result: The values of 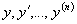 at
all iteration points corresponding to xout (for display etc.)
at
all iteration points corresponding to xout (for display etc.)
xout: The iteration points and the end point (for display etc.)
count: the number of iterations
If the value of 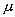 is set
in the van der Pol equation to increase the stiffness i.e. equation (3)
is changed to:
is set
in the van der Pol equation to increase the stiffness i.e. equation (3)
is changed to:
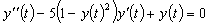 (5)
then this is mildly stiff and 4 d.p. accuracy can be achieved without increasing
the truncation parameter, N, at the cost of increasing the number of iterations
to 647. Any further increase in stiffness would require an increase in
N.
(5)
then this is mildly stiff and 4 d.p. accuracy can be achieved without increasing
the truncation parameter, N, at the cost of increasing the number of iterations
to 647. Any further increase in stiffness would require an increase in
N.
Example 2: The ODE
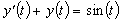
with initial conditions
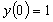
is calculated from 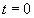 to
to 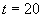 using the command:
using the command:
(6) -> solve([Y[1]+Y[0]-sin(X)],0.0,20.0,[1.0],1.0e-4)
and this produces:
(6)
[ifail: Integer, intensityFunctions:
List(String), method: Result,
result: Matrix(DoubleFloat),
y: Matrix(DoubleFloat),
xout: Matrix(DoubleFloat), explanations:
List(String),
x: DoubleFloat, count: Integer]
Type: Result
(7) -> %.y
(7) [0.252446658993222]
Type: Matrix DoubleFloat
in 176 iterations.
The same examples were solved using the Taylor series method incorporated
within Maple and using Runge-Kutta or Adams methods as appropriate within  both as the result only and with 200 intermediate results. The new algorithm
and the Maple symbolic algorithm were also timed including plotting the
resulting graph. The timings are as follows:
both as the result only and with 200 intermediate results. The new algorithm
and the Maple symbolic algorithm were also timed including plotting the
resulting graph. The timings are as follows:
| |
Example 1
|
Example 2
|
| Maple (Taylor)
including plot |
197s
795s
|
14s
153s
|
| ANNA (result only)
Intermediate results |
37s
65s
|
7s
56s
|
| New Algorithm
Including plot |
66s
72s
|
14s
16s
|
Table 1: Sample Test Timings
Commentary: The above results require some explanation. The increase
in time needed for 200 intermediate results using  is due to the smaller step-size required. The Maple results are affected
by the difficulty to tailor results to a given precision but similar results
are obtained with a purely symbolic algorithm written in Axiom.
is due to the smaller step-size required. The Maple results are affected
by the difficulty to tailor results to a given precision but similar results
are obtained with a purely symbolic algorithm written in Axiom.
*All tests were carried out on a SUN Sparc Classic named `dictum' under
Solaris 2.5.1 at the University of Bath using Axiom 2.2 and Maple V release
4.00f to 4d.p.
A display function provided with the upgraded  package can then produce:
package can then produce:
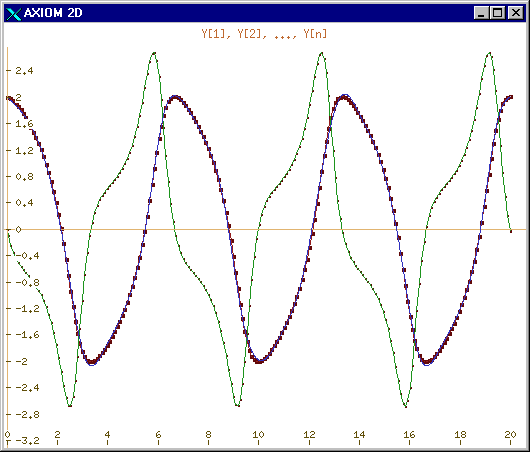
Figure 4: van der Pol's
equation with 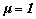 ,
, 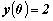 and
and 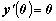 .
.
Initial Testing
Tests show considerable speed-up over purely symbolic processing, except
for the smallest of systems, but actual figures differ due to different
platform/platform combinations. However, the single most immediate effect
is of the simple interface and the amount of information returned. This
extra information is achieved at little extra cost.
With a non-stiff system, as equation (3), the accuracy of the system
is remarkable. If a variable loading is applied to affect the stiffness,
the accuracy drops dramatically unless the order of polynomial approximation
is increased. But this affects the time involved in the Fortran generation
stages. This means that for anything more than mild stiffness, the algorithm
is not optimal.
For simple systems, the cost can be comparable to other symbolic-numeric
methods as implemented within  ,
although the main benefits are in terms of the achieved accuracy and whether
intermediate results are required for, say, display. However, this method
is not appropriate to those ODEs for which the CAS cannot find the recurrence
relation.
,
although the main benefits are in terms of the achieved accuracy and whether
intermediate results are required for, say, display. However, this method
is not appropriate to those ODEs for which the CAS cannot find the recurrence
relation.
Incorporation
into ANNA
The incorporation of such a routine into  required the production of a measure function that calculates the system
size, stiffness and stability of the ODE and returns a value that corresponds
to the ability of this particular method to solve the ODE efficiently.
The databases also require updating.
required the production of a measure function that calculates the system
size, stiffness and stability of the ODE and returns a value that corresponds
to the ability of this particular method to solve the ODE efficiently.
The databases also require updating.
It is clear from the above that increasing stiffness will warrant a
larger polynomial approximation and therefore reduce the measure, up to
a point where a different method (such as BDF) would be more appropriate.
Similarly a larger system and decreasing stability would have the same
effect.
The measure function should also take into account that not all systems
of ODEs can be solved with this method: in particular, if the approximating
Taylor Series is difficult or impossible to calculate.
Tests have now been carried out with a range of systems of ODEs both
as a stand-alone algorithm and within  .
The algorithm has been shown to be reliable and, with the right conditions,
respectably efficient. With the right platform, for a huge number of classes
of ODEs, this method could become the method of preference.
.
The algorithm has been shown to be reliable and, with the right conditions,
respectably efficient. With the right platform, for a huge number of classes
of ODEs, this method could become the method of preference.
In the future it will be possible under certain circumstances to increase
the range of ODEs which can be solved by this method, such as where in
(1) 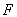 is not linear in
is not linear in 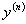 but a linear system can be calculated by differentiation. This could be
done within the pre-processing stages of the algorithm. The other area
which would need attention if this method is to be widely useful, especially
for real-world problems i.e. extremely large systems, would be the Fortran
generation tools within Axiom. It is the slowness of this part of the algorithm
that is dominating the evaluation. Only when this has been improved would
there be any benefit from using a better evaluation algorithm such as Horner.
but a linear system can be calculated by differentiation. This could be
done within the pre-processing stages of the algorithm. The other area
which would need attention if this method is to be widely useful, especially
for real-world problems i.e. extremely large systems, would be the Fortran
generation tools within Axiom. It is the slowness of this part of the algorithm
that is dominating the evaluation. Only when this has been improved would
there be any benefit from using a better evaluation algorithm such as Horner.
We expect to make the code available to Axiom users within a few months
of completion (September 1999) and final testing.
Graphical
Features
Adding graphical features to  ,
other numerical processes and new algorithms adds considerably to the understanding
of results, methods and the underlying mathematics. To this end, all of
the new algorithms use graphical feedback as is shown in Figure
2 and Figure 4.
,
other numerical processes and new algorithms adds considerably to the understanding
of results, methods and the underlying mathematics. To this end, all of
the new algorithms use graphical feedback as is shown in Figure
2 and Figure 4.
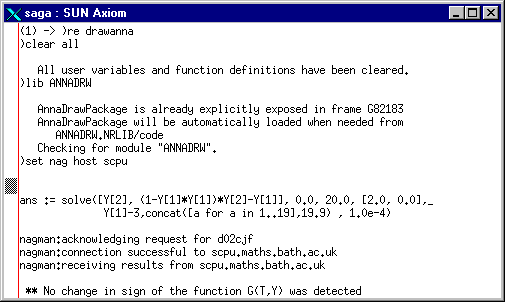
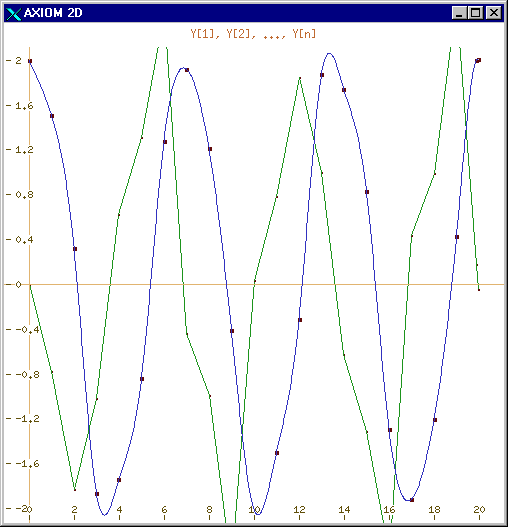
Figure 5: Graphical Output
for  Differential Equations
Differential Equations
The implementation of the display packages have entailed a further upgrade
of  (beyond that supplied
to NAG for inclusion into Axiom 2.2). The extra display routines cover
a wide range of the output from
(beyond that supplied
to NAG for inclusion into Axiom 2.2). The extra display routines cover
a wide range of the output from  ,
both in terms of the display of numerical output from the NAG routine,
and the ability to display input data.
,
both in terms of the display of numerical output from the NAG routine,
and the ability to display input data.
Since the range of output data types is dependent on the routine that
had been chosen for the solution of the given problem, and on the type
of problem itself, the packages need to distinguish the problem, the type
of problem and the numerical output before any particular display package
can be called. The upgrade to  was in the dynamic storage of this information.
was in the dynamic storage of this information.
Output packages have already been implemented for the ODE and Optimization
chapters of  and routines
for the Integration chapter are under construction. Figure
5 shows this package applied to the ODE of Figure
4 (van der Pol's equation) using ten intermediate points
for calculation of the spline representing
and routines
for the Integration chapter are under construction. Figure
5 shows this package applied to the ODE of Figure
4 (van der Pol's equation) using ten intermediate points
for calculation of the spline representing 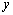 and simple straight-line fit for
and simple straight-line fit for 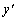 (the method will calculate many more points than this but for this example
only ten are needed for the spline interpolation).
(the method will calculate many more points than this but for this example
only ten are needed for the spline interpolation).
The solution of a system of ordinary differential equations is generally
of the form
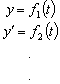
We therefore need to plot 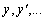 against time
against time 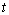 . This we can
do on a single graph. However, usually the most important values are given
by
. This we can
do on a single graph. However, usually the most important values are given
by 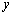 and so we not only plot
the values but also perform some interpolation on those values by drawing
a spline through the given points (and hide the Axiom straight-line fit).
and so we not only plot
the values but also perform some interpolation on those values by drawing
a spline through the given points (and hide the Axiom straight-line fit).
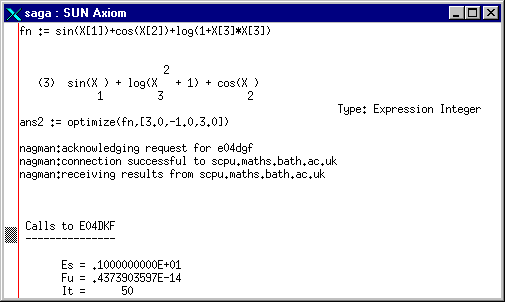
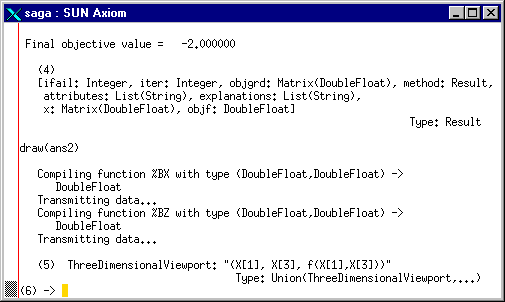
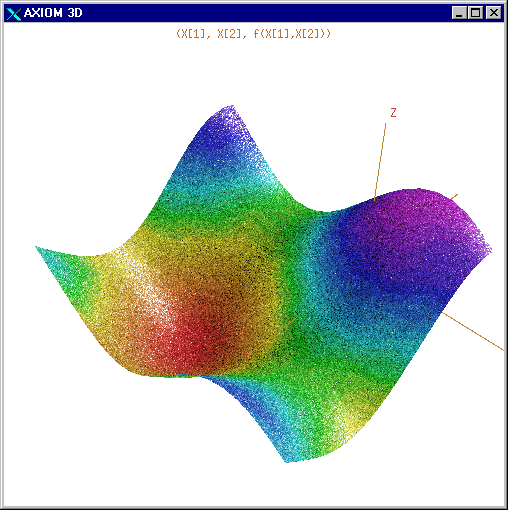
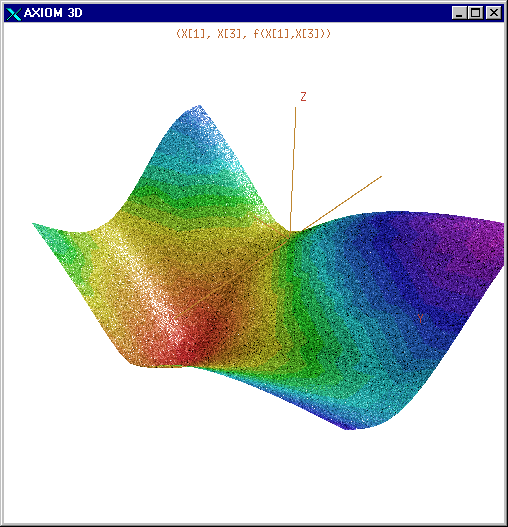
Figure 6: Graphical Output
for  Optimisation
Optimisation
Figure 6 shows representations of the function
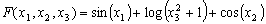
on two surface plots (obviously we cannot represent it as a four-dimensional
surface):
-
plot 6.1 shows the function
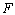 plotted against
plotted against 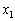 and
and 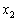 for
for 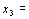 the minimum found by
the minimum found by 
-
plot 6.2 shows the function
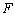 plotted against
plotted against 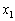 and
and 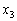 for
for 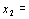
the minimum found by  .
.
Each of these plots also show the minimum point. Further options are
available for different combinations. In general, given the output from  and a list of variables, the routines plot the first variable against each
of the others in turn. If only one variable is required, the output is
a two-dimensional plot.
and a list of variables, the routines plot the first variable against each
of the others in turn. If only one variable is required, the output is
a two-dimensional plot.
Interpolation
Package
Introduction
Traditional methods of teaching mathematics in Universities split the
subject into discrete elements. For example, within the Escuela Técnica
Superior de Ingenieros Industriales there are courses in the Undergraduate
Program for Calculus, Linear Algebra, Differential Equations and Mathematical
Models and Methods. Within the Department of Mathematical Sciences at the
University of Bath, there are many more subdivisions. In general, these
courses are separate, maybe even modular, and taught by different members
of staff using different techniques and sometimes different notation. There
is usually little attempt to unify or compare such mathematical branches.
The same is generally true in algorithm design. Experts within the field
of Computer Algebra will often consider as appropriate only algebraic methods.
They will therefore tend to teach these methods to the exclusion of others.
Conversely, Academic Engineers will rather teach Fourier approximation
methods than consider exact analytical methods since the mathematics is
considered to be easier (or, more likely, that the process by which answers
to specific problems can be solved is easier to explain). It is to this
problem that this section is addressed.
In the Department of Mathematical Sciences at Bath, undergraduate students
have a choice (over their three/four years of study) of 47 taught courses
with mainly mathematical content (excluding Probability, Statistics and
Computing courses). In general, these courses can be grouped together into
the main branches of mathematics (Analysis, Linear Algebra, Differential
and Integral Forms etc.) and so have a lesser number of different course
needs and expectations. Thus some degree of insistence on the attending
of pre-requisite courses is assumed. However, this still leaves a large
number of different approaches to mathematics and mathematical thought
which have different requirements in terms of methods and notation.
It is therefore difficult, in both practice and theory, to unify or
bring closer such diverse mathematical disciplines. The student (and tomorrow’s
lecturer) is left with the understanding that cross-disciplinary techniques
neither exist nor can be understood. The examination process tends to reinforce
this conclusion since once the student has completed any particular course,
much of the content of that course is either no longer required in subsequent
courses, or is taught again (sometimes with different techniques and notation
such that the links are obscured).
Engineering students have a further semantic block. They tend to see
the world in terms of problems and the tools to fix those problems. "For
the vast majority of students mathematical knowledge consists of isolated
facts and procedures with only a few weak links between them" [Hubbard,
1997]. For them, the lack of understanding comes from the isolation of
mathematical ideas which are connected neither to each other nor to any
physical contexts. [Mitchelmore & White, 1995].
The aim of this section is thus to show that, where appropriate, such
links can be made, comparisons are useful and that a modern Computer Algebra
System has sufficient power and facilities to be of significant use in
giving students greater understanding of the breadth of mathematical design
[Dupée et al., 1999]. As a small example, we will introduce a learning
package, which can compare and contrast different methods, both symbolic
and numeric, of calculating interpolating functions. With the use of such
a package, the student will be able to compare and contrast the different
types of algorithms available to the mathematician and thus introduce them
to the interpretative process.
Interpolating
Functions
The classical forms of interpolating functions are polynomials. The
obvious reasons for this are that such functions are often easy to calculate
and easy to work with (differentiation of polynomials is elementary). The
standard and easily defined such function is the Lagrange Polynomial. There
exist, however, different algorithms for its calculation, the efficiency
of which is dependent on certain aspects of the input data points and on
accuracy requirements (if they can be defined).
So apart from the basic Lagrange algorithm, there are divided difference
algorithms (such as Newton), centred difference algorithms (Gauss and Stirling)
and iterated formulae (Aitken). Under some circumstances, many of these
will give the same result as the Lagrange formula.
In practice, simple polynomials can sometimes be considered impractical,
especially those of higher degree, in this case those calculated from a
large number of points. This is due to their oscillatory nature. A larger
number of input points may not improve the accuracy of the interpolation,
especially if there exist possible errors in the input data.
Instead of assuming that interpolating a function is best with a single
polynomial of high degree, algorithms for splines and Hermite interpolation
produce piece-wise cubic polynomials which are constructed in such a way
that the joints maintain certain defined properties. Hermite polynomials
rely on further knowledge of the differential at each of the input points
as well as the value. However, certain assumptions can be made using the
Lagrange derivatives such that a good fit can be achieved with a small
number of points. The NAG numerical routine E01BEF
calculates piece-wise cubic Hermite polynomials for best accuracy.
It is also possible to interpolate a function using non-polynomials,
such as rational functions (Bulirsh-Stoer) and trigonometric functions
(FFT). The algorithms for all of these methods can be found in many good
textbooks on Numerical Analysis such as [Burden & Faires, 1997] and
[Conte & de Boor, 1980].
Many of these algorithms are appropriate for symbolic code but, due
to the complexity of some of these algorithms, it is sometimes better achieved
numerically. Also, the mathematics involved in these algorithms draws on
a number of different disciplines. It is thus appropriate, as a test example,
for a learning package showing symbolic, numerical and graphical features.
Indeed, this provides one of the rare opportunities to demonstrate the
use of diverse mathematical processes.
The
Package
The package is written in Aldor [Watt et. al., 1995], the object-oriented
programming language designed for the Axiom Computer Algebra System [Jenks
& Sutor, 1992]. Thus it uses Aldor domains and categories with library
functions provided by Axiom. Axiom also provides the link to enable the
calling of routines from the NAG Numerical Library, the output graphical
facilities and the hypertext model, HyperDoc, for the user interface (tutorial
package) [Tapia et. al., 1998].
Inputs
The user can define the input function by:
-
a list of points i.e. a list of value pairs of the Axiom type Point;
-
a text file containing values;
-
a segment for automatic calculation of equidistant points;
Full flexibility is allowed for the function definition using combinations
of the above as below. This allows the user, and the worksheet designer,
to make comparisons on a variety of different types of problems, both large
and small.
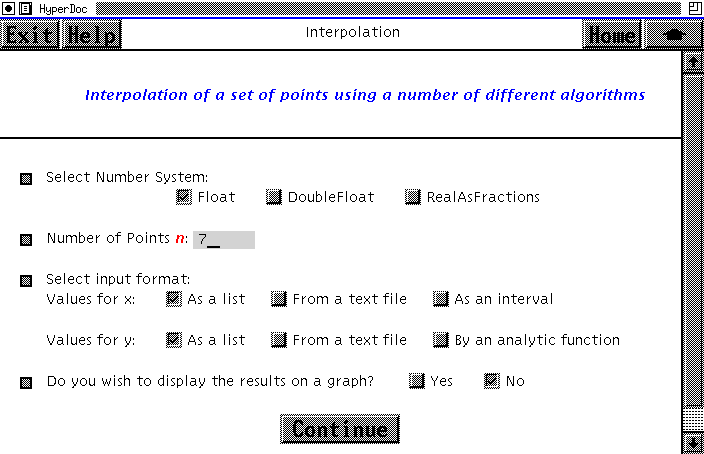
Figure 7: Opening HyperDoc Page
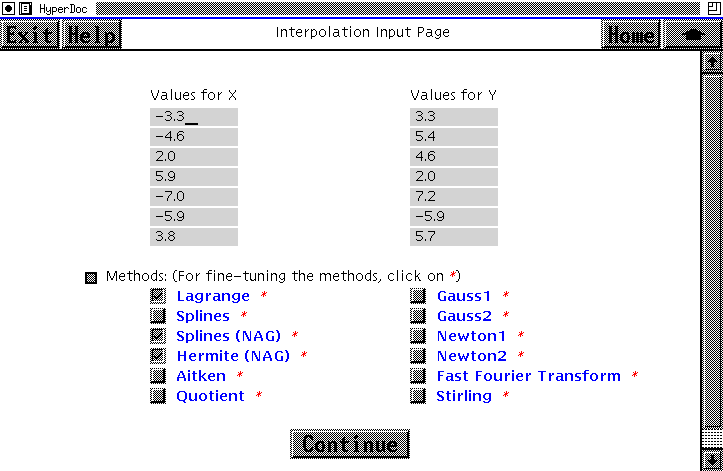
Figure 8: HyperDoc Input Page
Control Facilities
User control is given over a number of facilities for modifying the
process—either modifying the computing algorithm or modifying the calculated
output type. It is also possible to compare any modification directly with
the unmodified form i.e. use the same method a number of times with different
modifications.
For all methods it is possible to compare interpolation functions with
or without certain points suppressed. With polynomial methods one can specify
the variable (maybe for later use), and in the central difference methods
the central (start) point can be modified.
For the standard Lagrange method it is also possible to specify the
degree of the output polynomial by asserting zero values for particular
coefficients. For example, given 12 points as input, we can specify that
the coefficient of, say, 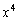 is
zero which will have the effect of making the output interpolating polynomial
of up to degree 12 instead of 11. Some of these coefficients may be negligible
if the calculation is made using double-precision floating-point numbers
but that is due to round-off error etc.
is
zero which will have the effect of making the output interpolating polynomial
of up to degree 12 instead of 11. Some of these coefficients may be negligible
if the calculation is made using double-precision floating-point numbers
but that is due to round-off error etc.
For the spline routine, it is possible to specify conditions on the
second derivatives at the end points.
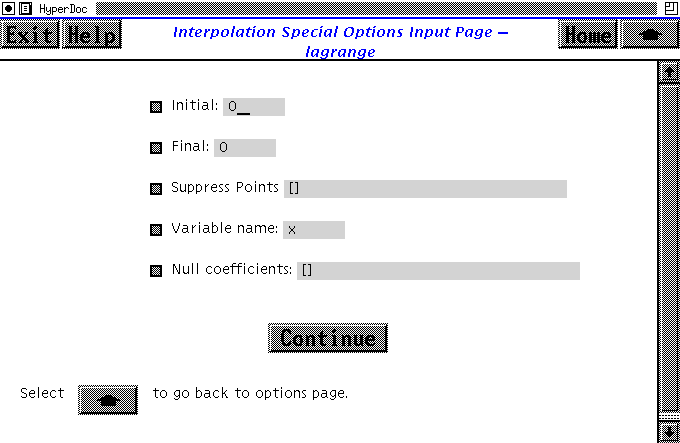
Figure 9: Options Page

Figure 10: Options Instigation Page
Graphical Display
Figure 11 shows how Axiom can display the output
interpolating functions. The functions are colour coded and can be removed
or highlighted as required, so that reasonable comparisons can be made.
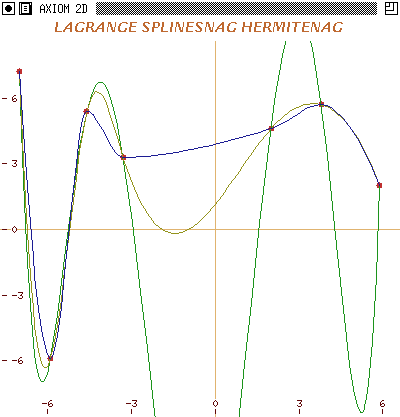
Figure 11: Output Graphical
Display
User Interface
It is envisaged that, when used as a learning package/tutorial, the
main user interface will be via the HyperDoc pages as shown in this paper.
This automatically formulates the correct command for supplying to the
command window as shown below.

Figure 12: Interpolation Instigation Page

Figure 13: Axiom Command Window
The user can then evaluate the interpolating functions at a given point,
draw the functions or even, if a function is a polynomial or rational function
(quotient of polynomials), analyse that function.
Output Functions
The output is in the form of a list of interpolating functions, which
can then be evaluated at a desired point, displayed as a graph or used
within further code. These interpolating functions could therefore take
the form of:
-
polynomial functions (Lagrange, Newton etc.);
-
piece-wise cubic polynomials (splines);
-
rational functions (Bulirsh-Stoer);
-
complex polynomials (fast Fourier transform);
-
composite functions i.e. functions which themselves contain calls to a
NAG routine for evaluation (splines, Hermite).

Figure 14: Output Functions
The
Learning Package in Use
The doctoral programme for which this package was designed contains
a course on Numerical Methods. A section of this course relates to interpolation
and interpolation techniques. As a practical part of this section, the
programme directors have created a student worksheet containing a sequence
of exercises to be completed (see Example Problems, page *)
along with a discussion of various issues relating to the different methods
and their uses. It is introduced to the students as part of a lecture.
The structure allows the students to both work at their own pace and
to use the exercises as a project of discovery, that is as an entry into
the Learning Cycle.
On each of the individual exercises the student is encouraged to modify
some of the parameters and compare the results in order to identify certain
characteristics of each method. One of the later exercises is a chance
for the student to create an example of their own to show more clearly
one of the characteristics thus found. All of this is then set down on
a student project report.
Conclusions
and Further Work
Although this is a new package and has only been in use at the Escuela
Técnica Superior de Ingenieros Industriales of the Universidad Politécnica
de Madrid one year and therefore feedback from the students is a little
patchy, the outlook for such a package is good. A number of improvements
have been identified, particularly in the syntax of the commands even though
such commands are, for the most part, automatically generated by the HyperDoc
interface.
So, before general release of this package to the wider audience, a
number of alterations will be made. One of these will be provision for
the input of data in the form of a variable i.e. from points previously
generated within the Computer Algebra System. This will further extend
the flexibility of the product.
The use of the package in the postgraduate course has shown the importance
of two features of the package. The first is the possibility of graphical
representation of every interpolating function, separate or together with
some other function chosen by the student. This feature allows the interpretation
of strange behaviour for a given set of points (as in Example 3 below)
and also the comparative analysis of different interpolating functions
for specific input data. As such, it is also a necessary part of the discovery
process – a skill unusual in the curriculum, since "in order to connect
new ideas to existing ones the student needs to be involved in activities
which assist in the connection building process" [Hubbard, 1997].
Another feature facilitating the easy use of the package by the students
is the two methods of data input—by means of the Axiom command-line interpreter
and using the HyperDoc interface. If the command is very large, it is better
to use the HyperDoc, in this case the command appears automatically in
the interpreter window. For the occasions that the student wants to alter
some data it is easier to use the window review/copy/paste facilities.
It is clear to the authors that provision must be made by the course
designers for this type of activity. The costs in terms of time would not
be great but the benefits should be noticeable.
The authors hope that the package will be completed and become available
from the NAG/Axiom website within a year.
Example
Problem Sheet
Some of the exercises for students to solve using the package are the
following :
Computing Errors
Interpolate the function ex using the Lagrange method.
Modify the intervals and compute the maximum error values in the interval 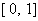 ,
choosing several degrees for the polynomials.
,
choosing several degrees for the polynomials.
Describe the relation between the distribution of points at the interval
and the error obtained for the interpolating function.
Error in Tabulated Values
Given the polynomial 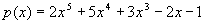
Evaluate 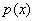 for
for 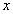 ?
? 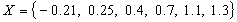 .
.
Compute the rational, Lagrange and spline (or another piecewise) interpolation
functions corresponding to the above set of x-values and the y-values obtained
previously but applying truncation on the second digit.
Incorporate a random point within X and calculate the new rational
interpolation function.
Compare with the first rational interpolation function and analyse the
results.
The Runge Phenomenon
Given the analytic function:
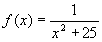
in the interval 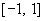 ,
,
Interpolate the function 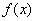 ,
using any polynomial interpolation and 15 equally spaced points. Draw the
result.
,
using any polynomial interpolation and 15 equally spaced points. Draw the
result.
Interpolate the same function at 30 equally spaced points. Compare the
error with the previous case. Draw the result.
Runge Phenomenon [Runge, 1901]: this time employ over 40 points and
display the result. What has happened?
Try a piecewise method (Hermite or splines) to interpolate the same
function at over 40 points.
The Aitken method implemented in the package has a stop condition, so
the resulting polynomials do not increase the degree if the error increases.
Try using the Aitken method and compare the results with above.
Try to find another example of the Runge Effect.
Interpolation of a Periodic Function
Given the analytic function:
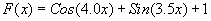
in the interval 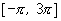 ,
,
Interpolate function 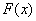 ,
using Fast Fourier Transform and splines at 8, 16 and 32 points. Display
the results and describe the different behaviour the two methods when increasing
the number of points.
,
using Fast Fourier Transform and splines at 8, 16 and 32 points. Display
the results and describe the different behaviour the two methods when increasing
the number of points.
Explain the different between the two methods in the central region
with 16 points.
Try other number of points and explain the results.
What will happened if we try any Lagrangian method at 16 points? Check
it.
-
Dissemination
The Interpolation package described above was presented in two major
conferences in 1998 i.e. the IMACS conference Applications of Computer
Algebra (IMACS-ACA '98) in Prague, Czech Republic, August 9--11, and the
International Conference of Mathematicians (ICM '98) in Berlin, August
18-27.
The paper presented at IMACS-ACA '98, "Composite Algorithms in the Teaching
of Mathematical Methods", was also published in a special edition of the
International Journal of Computer Algebra in Mathematics Education.
A paper, "Using a Computer Algebra System to Provide a Better Interface
to Numerical Routines", was presented at the 6th Rhine Workshop
on Computer Algebra, Bonn, Germany, 31 March – 3 April, 1998.
We presented a paper, "An Automatic Symbolic-Numeric Taylor Series ODE
Solver", at the international conference Computer Algebra in Scientific
Computing in Munich, Germany, May 31 -- June 4, 1999. It was also be published
in the Springer-Verlag series Lecture Notes in Computational Science and
Engineering.
A further paper was presented at IMACS-ACA '99 in El Escorial, Madrid,
Spain, 25 -- 27 June, 1999 entitled "Prototyping Symbolic-Numeric Algorithms
using Naglink".
The results of the project have also been presented at seminars at the
Universities of Bath, Cork, Bangor and at Napier University.
-
Bibliography
[Barton, 1980] Barton, D., "On Taylor Series and Stiff Equations", ACM
Trans. Math. Softw. (6), 3, Sept. 1980, pp. 281--294.
[Barton et al., 1971a] Barton, D., Willers, I. M., and Zahar, R. M.
V., "The Automatic Solution of Systems of Ordinary Differential Equations
by the Method of Taylor Series". Computer Journal (14), 3, 1971.
[Barton et al., 1971b] Barton, D., Willers, I. M., and Zahar, R. M.
V. "Taylor Series Methods for Ordinary Differential Equations --- an Evaluation".
In [Rice, 1981], pp. 369--390.
[Brougham et al., 1991] Broughan, K. A., Keady, G., Robb, T., Richardson,
M. G., and Dewar, M. C., "Some Symbolic Computing Links to the NAG Numeric
Library". SIGSAM Bulletin (25), July 1991, pp. 28--37.
[Burden & Faires, 1997] Burden, R.L. and Faires, J.D. "Numerical
Analysis", 6th ed. Brooks/Cole, Pacific Grove, CA., 1997.
[Conte & de Boor, 1980] Conte, S.D. and de Boor, C., "Elementary
Numerical Analysis: An Algorithmic Approach". McGraw-Hill, New York. 1980.
[Corliss & Chang, 1982] Corliss, G. F., and Chang, Y. F., "Solving
Ordinary Differential Equations Using Taylor Series"., ACM Trans. Math.
Softw. (8), 2, June 1982, pp. 114--144.
[Dewar, 1994] Dewar, M. C., "Manipulating Fortran Code in AXIOM and
the AXIOM-NAG Link"., In: Workshop on Symbolic and Numeric Computation
(1993)(Helsinki, 1994), H. Apiola, M. Laine, and E. Valkeila, Eds., pp.
1--12. Research Report B10, Rolf Nevanlinna Institute, Helsinki.
[Dupée &
Davenport, 1996] Dupée, B. J., and Davenport, J. H., "An Intelligent
Interface to Numerical Routines., In: DISCO'96: Design and Implementation
of Symbolic Computation Systems (Karlsrühe), 1996, J. Calmet and
J. Limongelli, Eds., Vol. 1128 of Lecture Notes in Computer Science, Springer
Verlag, Berlin, pp. 252--262.
[Dupée & Davenport, 1999] Dupée, B. J., and Davenport,
J. H., "An Automatic Symbolic-Numeric Taylor Series ODE Solver", in: CASC’99:
Computer Algebra in Scientific Computing (München), 1999, V. G.
Ganzha, E. W. Mayr and E. V. Vorozhtsov, Eds. Springer Verlag, Berlin,
pp. 37—50.
[Dupée et al., 1999] Dupée, B. J., Martínez, R.
& Tapia, S., "Composite Algorithms in the Teaching of Numerical Methods",
International Journal of Computer Algebra in Mathematics Education, (6)
1, 1999, pp. 51—64.
[Heck, 1996] Heck, A., "Introduction to Maple", 2nd ed. Springer
Verlag, New York, 1996.
[Hubbard, 1997] Hubbard, R., "Designing Questions that Develop Understanding".
Int. J. Math. Educ. Sci. Technol, (28) 6, pp. 793-810. 1997.
[Jenks & Sutor, 1992] Jenks, R. D., and Sutor, R. S. "AXIOM: The
Scientific Computation System". Springer-Verlag, New York, 1992.
[Keady & Nolan, 1994] Keady, G., and Nolan, G. "Production of Argument
Subprograms in the AXIOM-NAG Link: Examples Involving Nonlinear Systems.
In: Workshop on Symbolic and Numeric Computation, May 1993 (Helsinki,
1994), H. Apiola, M. Laine, and E. Valkeila, Eds., pp. 13--32. Research
Report B10, Rolf Nevanlinna Institute, Helsinki.
[Mitchelmore & White, 1995] Mitchelmore, M.C. and White, P., Math.
Educ. Res. J. (7) 50-68. 1995.
[Norman, 1973] Norman, A. C., "TAYLOR Users Manual"., Computing Laboratory,
University of Cambridge, UK, 1973.
[Norman, 1975] Norman, A. C., "Computing with Formal Power Series".
ACM Trans. Math. Softw. (1) (1975), pp. 346--356.
[Norman, 1976] Norman, A. C., "Expanding the Solutions of Implicit Sets
of Ordinary Differential Equations". Comp. J (19) (1976), pp. 63--68.
[Rice, 1971] Rice, J. R., Ed. "Mathematical Software". Academic Press,
New York, 1971.
[Runge, 1901] Runge, C., "Über empirische Functionen und die Interpolation
zwischen aquidistanten Ordinaten". Zeitschrift für Mathematik und
Physik, 46, pp. 224-243. 1901.
[Tapia et al., 1998] Tapia, S., Martínez, R. and Dupée
B.J., "Interpolating Functions in Axiom".
Project Report. E.T.S.I.I., Universidad Politécnica de Madrid,
Madrid, Spain and Dept. of Math. Sci., University of Bath, Bath, UK. Composite
Computing Methods Integrating Symbolic, Numeric and Graphical Packages
for Research Engineers. 1998.
[Watt et al., 1995] Watt, S. M., Broadbery, P. A., Dooley, S. S., Iglio,
P., Morrison, S. C., Steinbach, J. M. and Sutor, J. S., "The Axiom Library
Compiler User Guide", NAG Ltd. Oxford, UK. 1995.
[Wolfram, 1996] Wolfram, S., "The Mathematica Book, 3rd ed.
CUP, Cambridge, 1996.
[Young & Gregory, 1988] Young, D.M. and Gregory, R.T. "A Survey
of Numerical Mathematics". Vol. 1. Dover, New York. 1988 Reprinted with
corrections. Originally published Addison-Wesley, Reading, Mass. 1972.
[Zwillinger, 1989] Zwillinger, D., "Handbook of Differential Equations",
2nd ed. Academic Press, San Diego, CA, 1989.
![]() for
Windows *
for
Windows *
![]() ,
developed under the previous project, with graphical packages for the display
of numerical and symbolic/numerical data, together with the implementation
of further algorithms and techniques using a combination of symbolic and
numerical methods.
,
developed under the previous project, with graphical packages for the display
of numerical and symbolic/numerical data, together with the implementation
of further algorithms and techniques using a combination of symbolic and
numerical methods.
![]() as an integral part. This version of
as an integral part. This version of ![]() has thus been upgraded to include better explanation and automatic tuning
mechanisms and underwent considerable testing as required by NAG.
has thus been upgraded to include better explanation and automatic tuning
mechanisms and underwent considerable testing as required by NAG.

![]() for Windows Integration Example
for Windows Integration Example![]() on the PC.
on the PC.

![]() on the PC. This
has been tested in Bath and at the Universidad Polytécnica de Madrid.
Since the system uses much altered technology and increased graphical display
and formatting possibilities, I have provided it with a range of graphical
interfaces, thus allowing us some idea of the uses to which we could put
the new system.
on the PC. This
has been tested in Bath and at the Universidad Polytécnica de Madrid.
Since the system uses much altered technology and increased graphical display
and formatting possibilities, I have provided it with a range of graphical
interfaces, thus allowing us some idea of the uses to which we could put
the new system.