Data Structures and Algorithms

Exam preparation, recap and revision

Substance

  • Data Structures
  • Algorithms

Data Structures

Linear

  • Arrays
    • resizable / dynamic arrays
  • Linked lists
  • Stacks and queues
  • Hashtables
    • Chaining
    • Open addressing

Tree-based

  • Trees!
  • BSTs
  • Self-balancing trees: AVL-trees
  • Heaps
  • Priority queue
  • Disjoint-sets

Algorithms

Sorting

  • selection sort
  • insertion sort
  • Shell sort
  • Merge sort
  • Quick sort
  • Heap sort

Tree and graph exploration

  • Tree traversals
  • Depth-first search
  • Breadth-first search
  • Dijkstra’s algorithm
  • Floyd-Warshall algorithm
  • Kruskal’s algorithm
  • diff

Cryptography

  • RSA

Concepts

Complexity

  • asymptotic complexity: O, Ω, Θ
    • worst case
    • average case

\[ 1 < \alpha(n) < \log n < n^\epsilon \] \[ n < n^2 < n^3 < \ldots < 2^n < 3^n < \ldots < 2^n \] \[ 2^n < 3^n < \ldots < 2^{2^n} < 2^{2^{2^n}} < \ldots < \mathsf{ackermann} \]

  • Amortized complexity of a sequence of operations
  • Calculating complexity (recap coming later)
    • master theorem

Algorithmic approaches

  • Divide and conquer
  • Trees create logs!
    • Master theorem case 2
    • heap for priority queue
    • AVL trees
  • Dynamic programming
    • avoid recomputing overlapping subproblems

Correctness

  • loop invariants

Recaps

Calculating complexity

How often is tick called? 

for (int i = 1; i < n; i++) {
    tick(); 
}

for (int i = 1; i < n; i++) {
    for (int j = 1; j < n; j++) {
        tick(); 
    }
}

for (int i = 1; i < n; i++) {
    for (int j = 1; j < i; j++) {
        tick(); 
    }
}

for (int i = 1; i < n; i++) {
    for (int j = n; j > 1; j = j/2) {
        tick(); 
    }
}

for (int i = 1; i < n; i++) {
    for (int j = i; j > 1; j = j/2) {
        tick(); 
    }
}

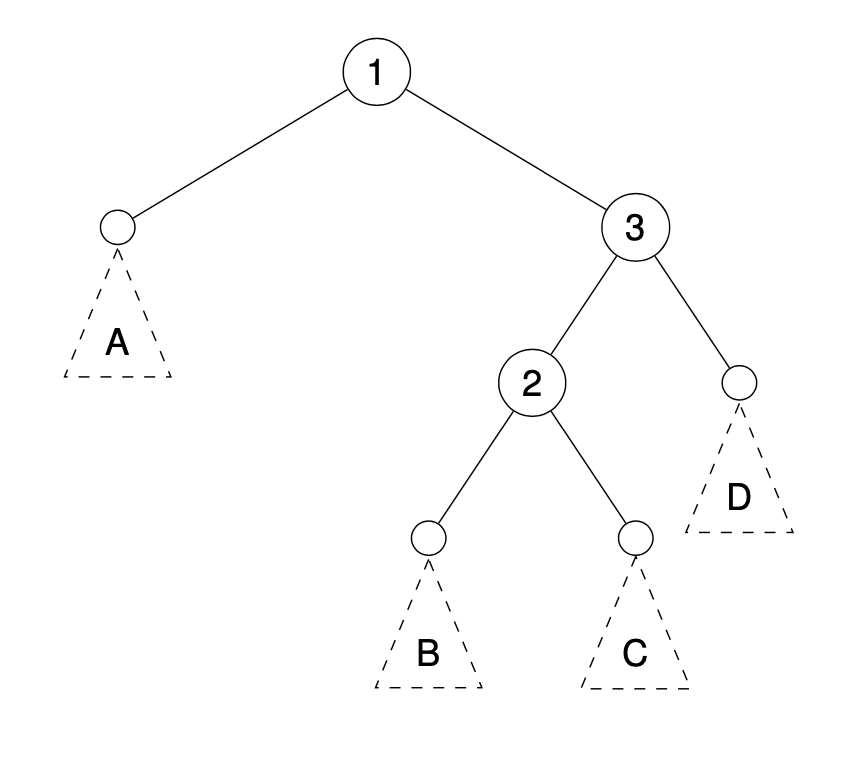
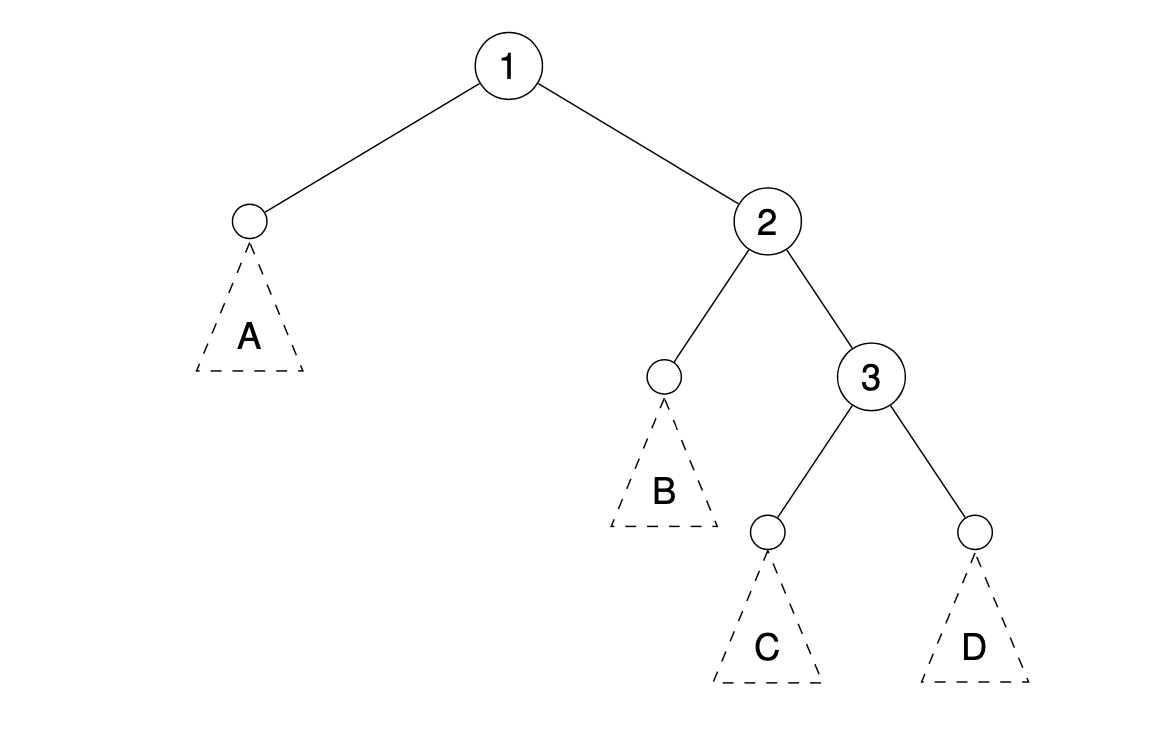
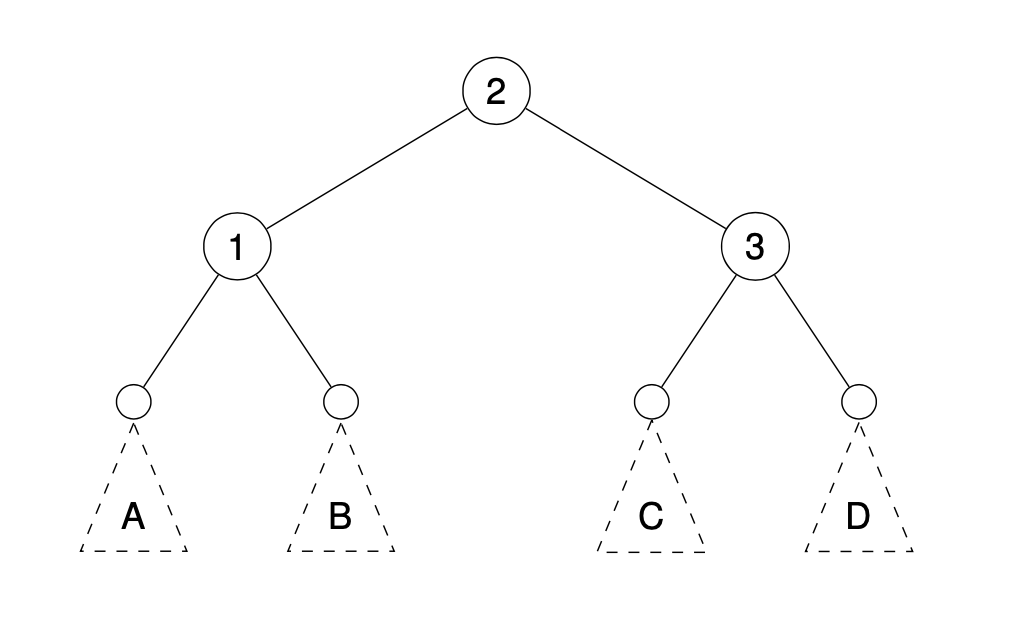
AVL Trees

An AVL tree is a BST satisfying the AVL condition: every node’s balance factor is 0, -1 or 1.

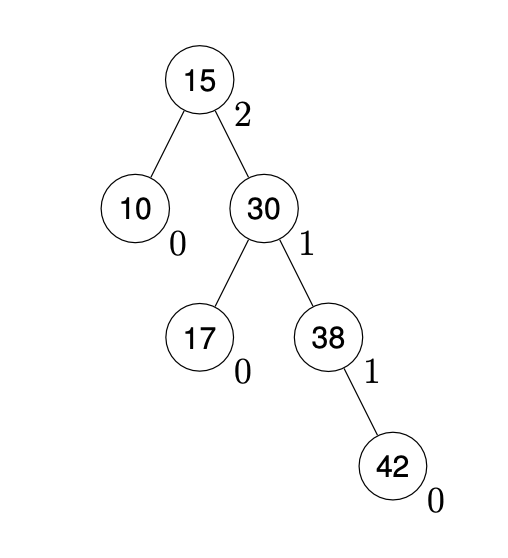
balance-factors.png

When nodes are added or deleted we may need to rebalance to maintain the AVL condition.

This is done using rotations.

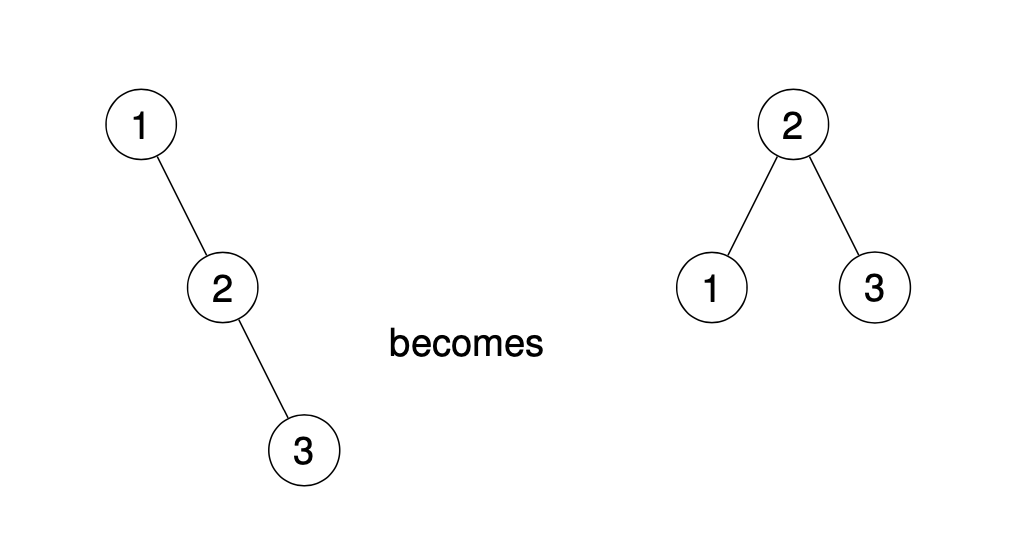
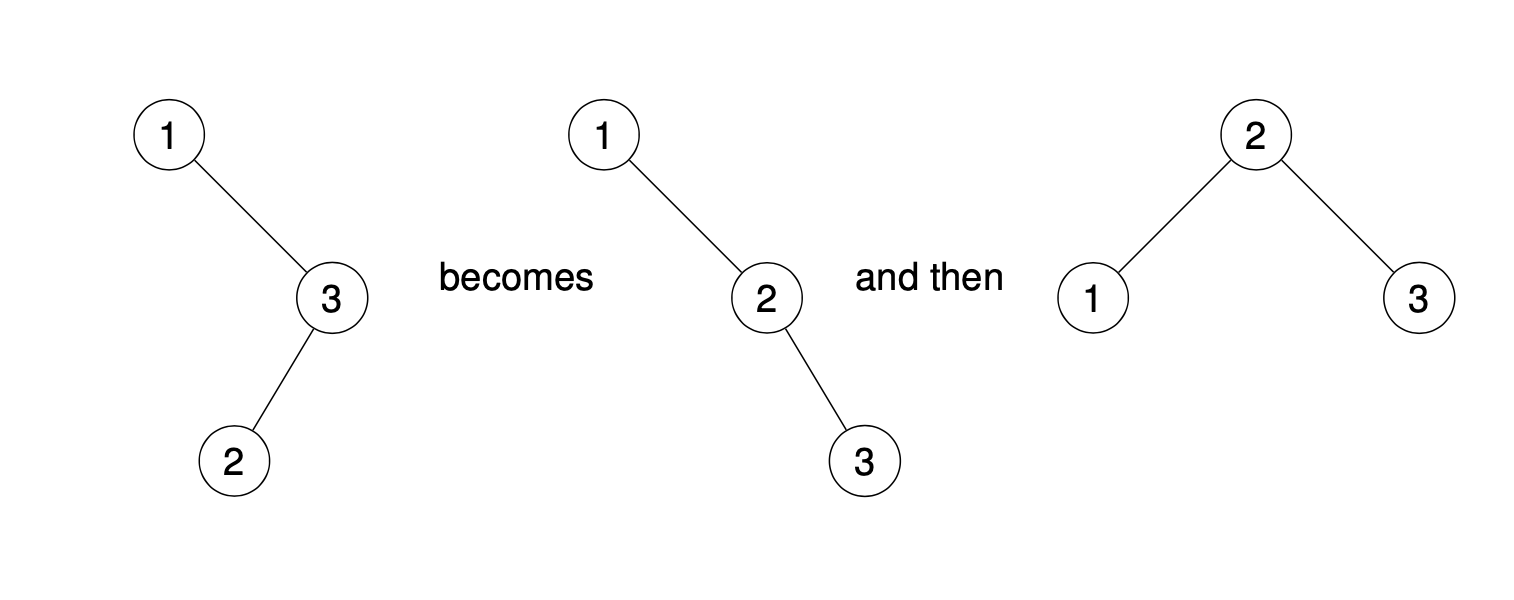
Tree rotations with no subtrees

rr-rotation-no-subtree.png

rl-rotation-no-subtrees.png

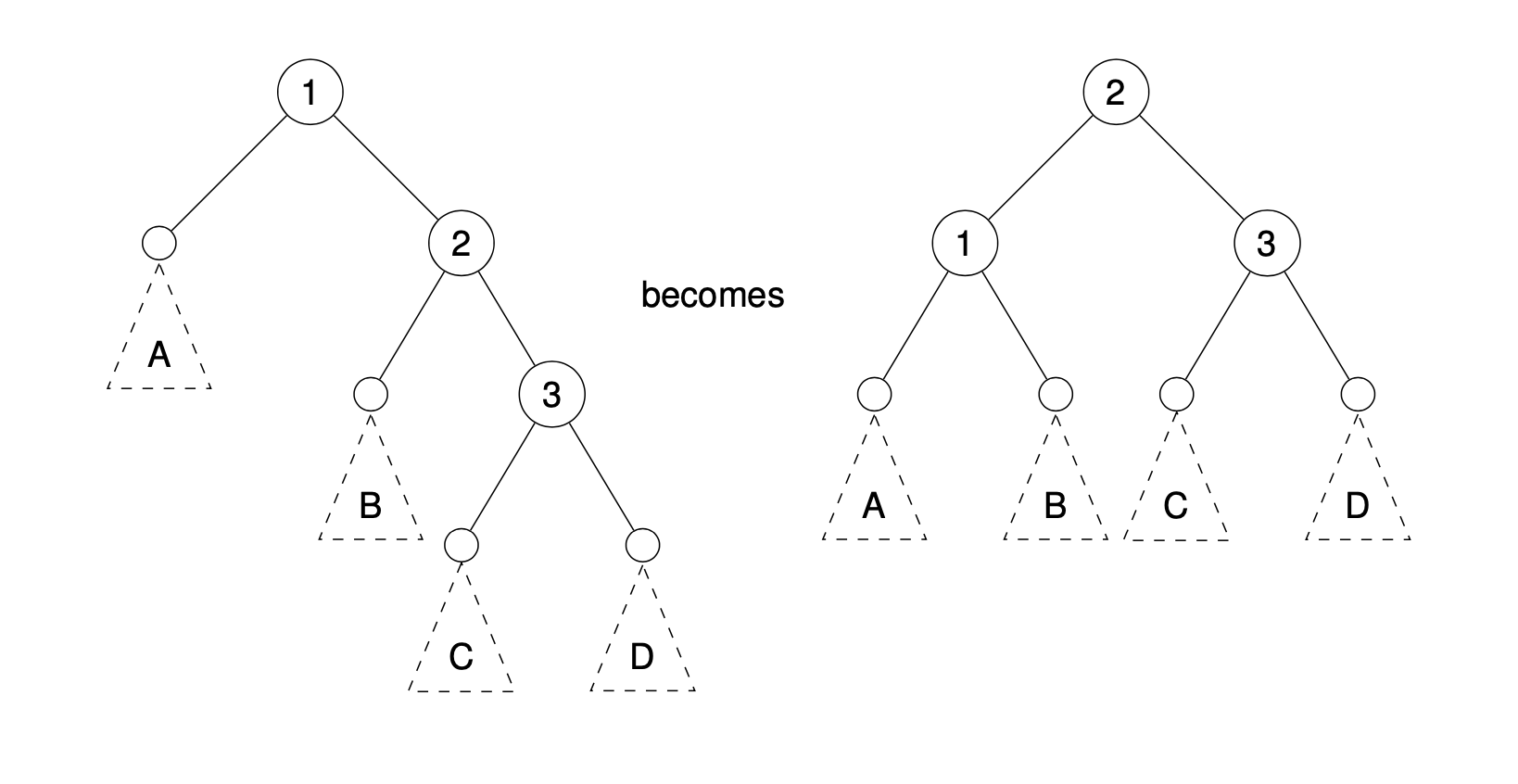
Adding subtrees

Do the same! Just make sure to place the subtrees in such a way that the inorder traversal is unchanged.

RR case: rr-rotation-with-subtrees.png

RL case:

rl-rotation-with-subtrees-1.png

rl-rotation-with-subtrees-2.png

rl-rotation-with-subtrees-3.png

Exam format

  • 8 multiple choice questions worth 20 marks total
  • 2 longer answer questions worth 20 marks each
  • Roughly 5 minutes per MCQ, 40 minutes for each longer question
  • Don’t expect to just glance at the MCQs and be able to answer them: some working is required – use the back of the answer book
  • Model paper is available on Moodle.
  • Please use the forum for questions, up to next Monday 16/1/2023.