home
| CV |
| Research |
| Teaching |
| Contact |
| NASA ADS link |
| Google Scholar link |
| Photography |
| Amusements |
| Useful Links |
| Protoplanetary Disk Resonances and Halting Type I Migration |
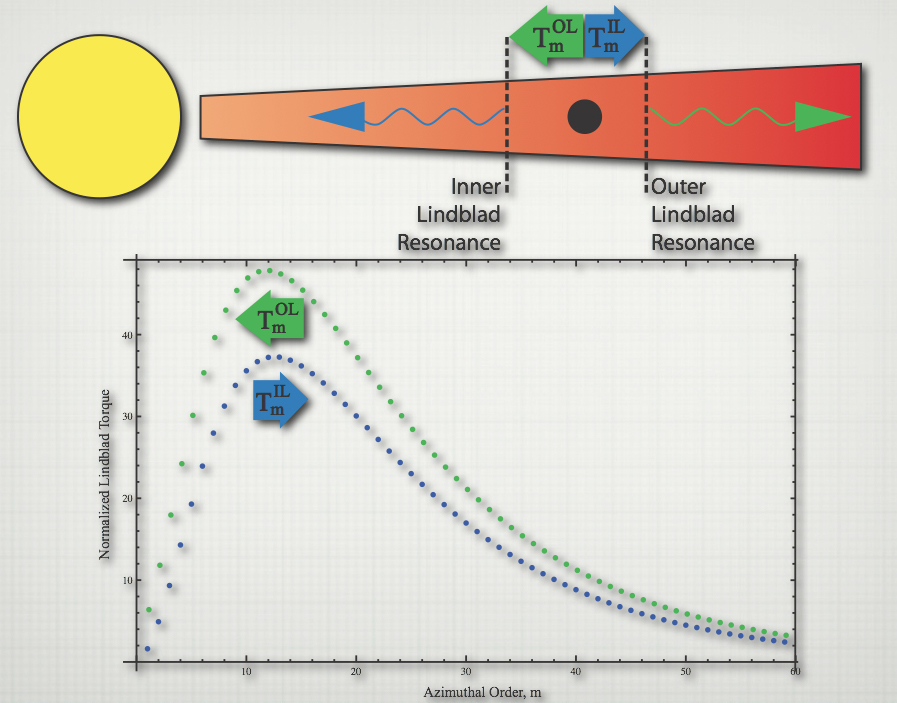
In a recent paper published in the Astrophysical Journal, I outlined a process by which Type I migration could be halted for small planets within a protoplanetary disk. Type I migration occurs when a planet is too small to clear a gap in the protoplanetary disk. The planet interacts gravitationally with the local disk material, launching waves from the "Lindblad" resonances, locations in the disk where the local epicyclic frequency of the gas/particulates is equal to the perturbation frequency due to the planet. Material at these locations are particularly susceptible to excitation by the planet because of this match in frequency. For each Fourier mode of the perturbation there are two Lindblad resonances, one inwards from the planet and one outwards from the planet. Waves launched from the inner Lindblad resonance carry away negative angular momentum (their pattern speed is slower than the background Keplerian rotation of the disk in the inner region, so higher amplitude waves reduce the net angular momentum of the system) and thus cause a positive torque on the planet driving it outwards. (Keplerian orbits have higher angular momentum the further out they are, thus positive torques tend to move things outwards.) Conversely, waves launched from the outer Lindblad resonance carry away positive angular momentum (their pattern speed is faster than the background keplerian rotation in the outer part of the disk), and thus apply negative torque on the planet, driving it inwards.
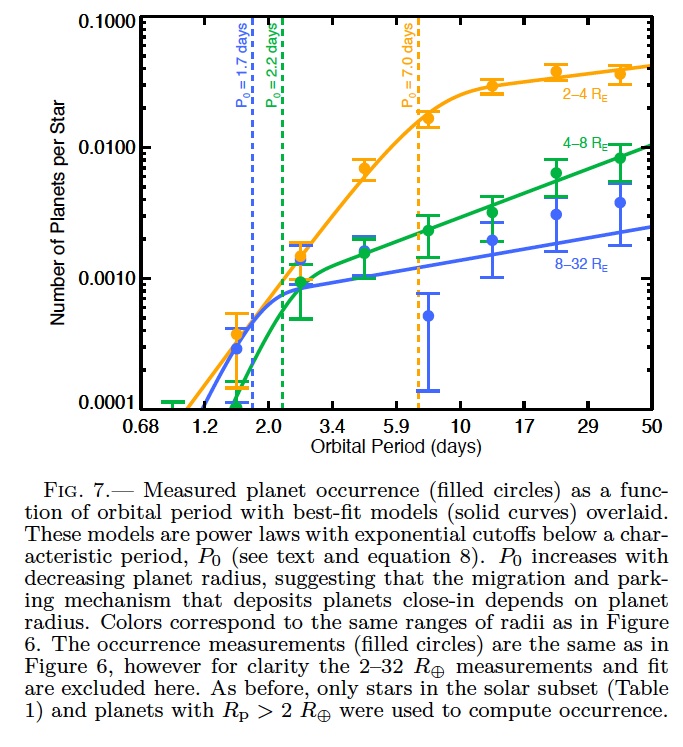
Typically, as shown in the plot above, the strength of the outer Lindblad torques (green) exceeds that of the inner Lindblad torques (blue) for each azimuthal Fourier mode "m" and the net migration is inwards. This process is what is known as Type I migration. (Type II migration occurs in a different regime when a planet is massive enough to clear a gap in the disk, and the planet and the disk become viscously locked.) Thus planets are driven inwards by interaction with the disk until they run out of disk to interact with and Type I migration turns off. The disk typically is truncated by magnetic activity of the star near to its corotation radius (where the keplerian rotation rate of the disk matches the spin rate of the star and its magnetic field). This typically happens for solar type dwarf stars at about 0.05 AU which corresponds to a period of about 4 days. Thus one might expect any planets that have been migrating primarily via disk interaction to be mostly stopped interior to roughly ~0.05 AU, such that no Lindblad resonances lie in the disk. However, the Kepler Mission recently returned a surprising observation about the distribution of planets very close to their host stars. A paper by Howard et al (2011) showed that there were two population in the radial distribution of planets, small planets (2-4 earth radii) had an exponential cutoff at about 7 day orbits, while larger planets (4-32 earth radii) had exponential cutoff at about 2 day orbits.
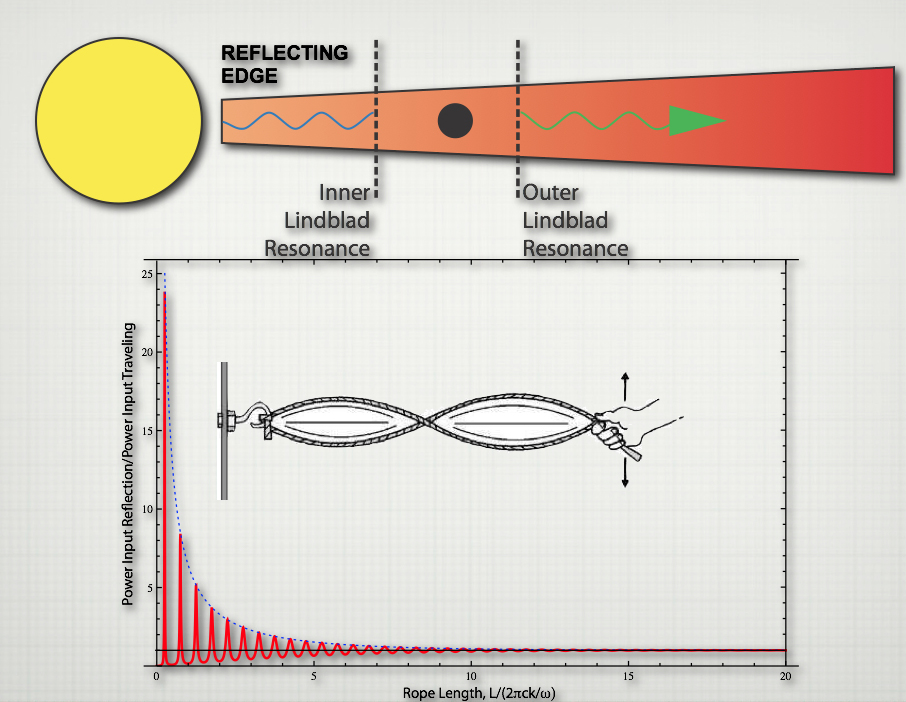
This result is somewhat surprising. It implies that there is a difference in the halting mechanism based on the size. but naively one would assume the halting mechanism (say tidal circularization after planet scattering) would have the opposite dependence on planet size. Smaller planets would interact less strongly with the host star and be able to move in more closely before being halted. In my work, I examine the effect of the inner disk edge on the torque due to the inner Lindblad resonance. If waves reflect off the inner edge of the disk, then they can bounce back and interact with the planet again. Waves that are resonant in this cavity can interact very strongly, and increase the torque. To understand this, it helps to consider the following toy problem: Imagine you have a rope with a free end that you are waving up and down with some fixed force amplitude and frequency. The power you are putting into the rope , the work you are doing per unit time to the rope is a certain value, given by the rate of energy flux the wave carries at it travels down the rope that you have excited. If instead you tie the rope to a wall at some length away and excite the rope in the same way you get the wave reflected back and resonance behavior as shown in the figure below.
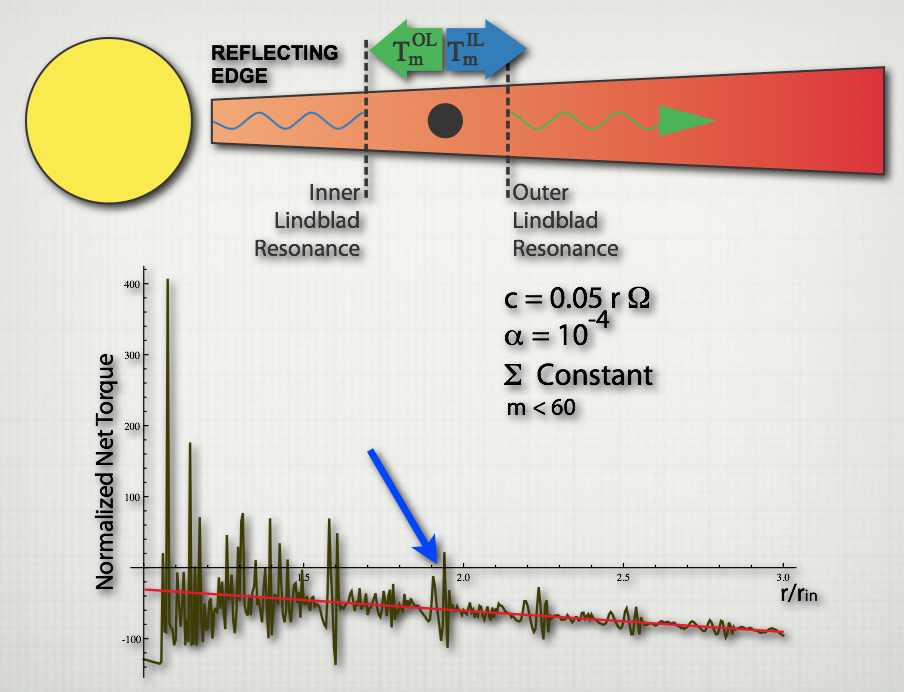
Here the plot shows the ratio of the power input into the rope system with a reflecting boundary condition over the power input in the system where the end of the rope is free and waves simply travel away from your hand. When the waves are resonant with the cavity, between the hand and the wall, then we have a strong spike in the power input. How large that spike is depends on how much friction is involved in exciting this rope. (In the unphysical frictionless case, the mode amplitude and power would be infinite.) Similarly we have the inner Lindblad torques magnified by a resonance factor if the waves reflected off the inner disk edge are resonant in the cavity. This amplified torque can counter the torque due to the outer Lindblad resonance, and if the resonance is strong enough, can lead to a net positive Lindblad torque at the resonant peak, If a planet migrates inwards into this peak, the positive torque will force it away, but as it moves away, the torque again becomes negative and the planet will be pushed outwards. In this way the planet becomes trapped where the net torque is approximately zero,
In the figure above a planet migrating inwards is trapped at a few times the inner radius by the resonant peak such that the net torque crosses zero. Hence: For larger planets this halting mechanism breaks down, as the waves become non-linearly dissipated. Above a certain cutoff mass, this disk resonance halting mechanism no longer functions and the planets can continue to migrate until the Lindblad resonances exit the disk. This naturally provides a mechanism which halts smaller planets slightly interior to the disk edge, while larger planets are halted by exiting the disk, closer to the star. This type of mechanism will also work near other reflecting edges in protoplanetary disks, like, for instance, the density transition edges of dead zones, or the gap edges near giant planets. Andrew Howard recently gave a talk at the first Kepler conference about the Patterns of Low-Mass Planet Occurence from Kepler and Doppler Planet Searches which featured my work. (Starting at ~21 minutes).
|