Click for linear version Click for slides Click, print preview and print slides

SpLDs and Maths

Bridging the Gap

Emma Cliffe

Mathematics and Statistics Resource Centre

Plan

Mind the gap!
SpLDs and mathematics
Anxiety and resilience
Mini needs assessment exercise
Technology, support methods and practical resources
Designing support exercise
Collaboration?
Discussion: What is the aim?
Further reading

Mind the gap!

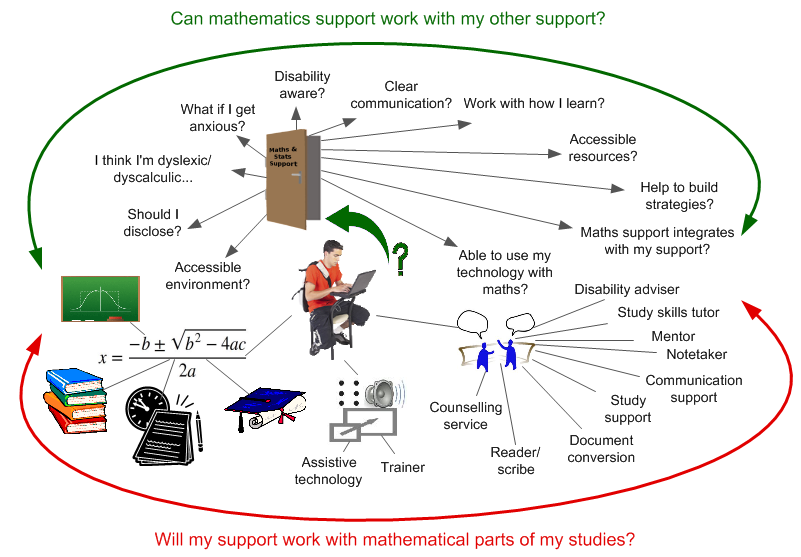
Diagram summarising concerns a student might have about how their support and mathematics support might work together.

SpLD support

This one to one support addresses the issues which some students might have in acquiring, recalling and retaining information in written and spoken language as well as the range of memory, organisational, attention and numeracy difficulties that students with specific learning differences often face when working in an HE context.

[...] This support should aim to develop students’ skills for autonomy in the learning environment. It should be tailored to a student’s individual needs [...]

SFE Non-Medical Help Services Reference Manual: http://www.practitioners.slc.co.uk/media/6192/non_medical_help_manual.pdf

Who does this?

Tutors hold membership of one of four professional bodies.

Degree
Recognised specialist Students with SpLD qualification
Teaching experience
Engagement with continuing professional development.
Mathematical fluency and confidence highly varied.

How is it delivered?

1:1, perhaps weekly, perhaps for an extended period
Planned with input from student, Educational Psychologist Report, Needs Assessment Report...
Collaboratively build tailored approaches towards independence

Mathematics support...

... is a recognised collective term for extra-curricular mathematics and statistics teaching and learning services

[...] The term covers activities, facilities and/or resources provided to support and enhance students’ learning of mathematics or statistics

[...] It is designed to assist students in developing mathematical and/or statistical confidence and skills.

[...] students are encouraged to help themselves and not rely solely on the intervention of a tutor

sigma Network:
http://www.sigma-network.ac.uk/about/what-is-mathematics-statistics-support/

Who does this?

Staff with a mathematics background and varying levels of pedagogical knowledge and support experience:

Teaching staff dedicated to the provision of extra-curricular maths support.
Lecturers/Teaching Fellows as part of teaching load.
Postgraduate tutors on casual basis.
Knowledge of SpLD support highly varied.

How is it delivered?

Dropin, workshops, group and 1:1 appointments
Little tailored planning - tutor must often respond to, perhaps complex or poorly formed, queries immediately
The student is there for maths help, often with a specific problem. Unpicking and responding to study skill gaps in real time is difficult and the student may not be receptive.

A tension within maths support

In a rushed dropin it is hard for us to stand back from the presented maths problem
The student expects that progress will be made on this
In the long run the student is better served by building skills and strategies towards independent learning and problem solving - SpLD support is based on this premise
But the student may not be receptive in this context
This tension is an issue I will come back to...

Mind the gap!

A student may not build effective and appropriate mathematics study skills for their degree.

Without which effectively acquiring mathematical information and skills independently is difficult.

Constant fire-fighting erodes confidence...

and may challenge a core identity of STEM students who "hated English but was good at maths and science".

SpLDs and mathematics

Neurodiversity...

is present when an exceptional degree of variation between neurocognitive processes results in noticeable and unexpected weaknesses in the performance of some everyday tasks when compared with much higher performances on a subset of measures of verbal and/or visual abilities for a given individual. These [...] include tasks of learning and remembering, time management, social interaction and attention span, as well as tasks requiring fine and gross motor movements

is a positive statement of differentiation

Grant, 2009. The psychological assessment of neurodiversity. Neurodiversity in higher education: Positive responses to specific learning differences, 33-62.

Dyslexia and mathematics

Maybe we could start by looking at some notes together?

Well, this important bit - what has it to do with conics?

a section of notes about canonical forms.

That moment of maths support fear: I have no idea...

What led you to think about conics?

Well, it says so, right there: "conical form"

The real fear

I can resolve the current query but do I have the requisite knowledge and skills to support the student in building strategies for independence? Do I know what other difficulties the student might encounter?

Dyslexia

Dyslexia mainly affects the development of literacy and language related skills. It is characterised by difficulties with:

Phonological processing
Rapid naming
Working memory
Speed of visual processing

This can result in difficulties with reading, writing, spelling, sequencing and memory. Areas of relative strength might include, for example, verbal comprehension, visual reasoning, and holistic, rather than sequential, processing.

Areas of difficulty in mathematics

Notes/solutions may contain copying errors, symbol confusion/reversals, word substitution or be incomplete
Reading errors. Working memory may be overloaded when processing conceptually abstract or multi-step material

Layout, font and style of "traditional" mathematics texts can add to processing difficulties

Difficulty forming and retrieving association between mathematical vocabulary, notation and concept
Difficulty learning, or producing from understanding, accurately stated definitions, theorems and formulae
Combining multiple aspects and sequencing in procedures, arguments or proofs can be challenging
May have difficulties moving from concrete to abstract

Dyspraxia and mathematics

Something my lecturer claimed about shapes makes no sense

Do you have a picture?

Apparently, this is cyclohexane in boat conformation

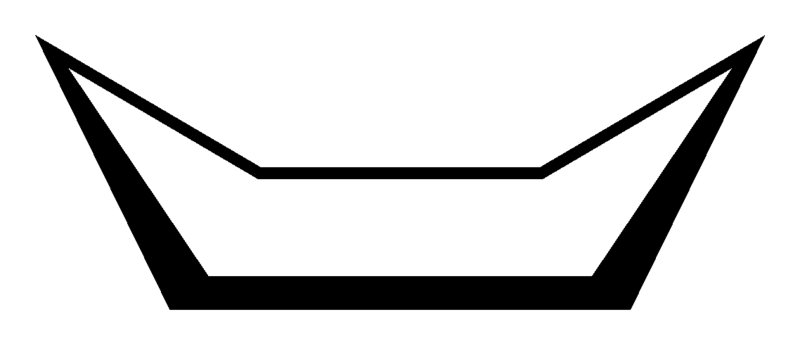
That moment of maths support fear as chemistry turns up

Can you see that it has the shape of a boat?

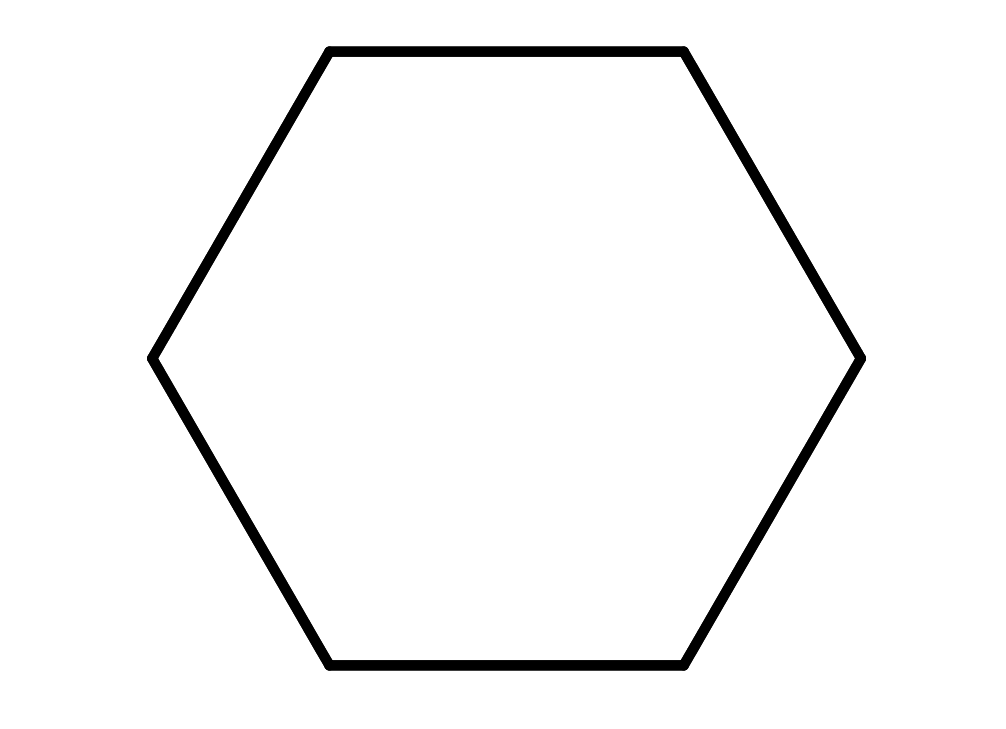
Yes, but cyclohexane is supposed to be a hexagon.

The real fear

Dyspraxia

Dyspraxia affects the planning of what you do and how you do it. It is associated with problems of perception, language and thought and is characterised by difficulties with:

Motor coordination, including handwriting, drawing etc.
Speed of visual processing
Visual reasoning
Working memory

This can result in difficulties with organisation, attention, spatial awareness, managing time and space, sequencing, memory and written expression. Areas of relative strength might include, for instance, verbal comprehension, verbal reasoning and 'out of the box' thinking.

Areas of difficulty in mathematics

May have similar difficulties with processing speed and working memory as experienced by students with dyslexia but reading/spelling not specifically weak
Spatial issues and weaker visual reasoning can have specific impacts e.g. geometry, concrete questions in 2D or 3D, seeing symmetry and structure
Notetaking/solutions may be very difficult to read back, inaccurate and incomplete
Drawings of figures etc. may be hard to follow
May produce non-standard solutions

Dyscalculia and mathematics

I'm preparing for the Numeracy skills test and I need help. How do I know what to do with this question?

question from teachers numeracy test practice paper 2

That moment of maths support fear: is there something in there to catch us out?

I see all the numbers, I become more and more anxious and I can't make any sense of it.

The real fear

Dyscalculia: definitions

Diagnostic and Statistical Manual of Mental Disorders IV:

"(A)s measured by a standardised test that is given individually, the person's mathematical ability is substantially less than would be expected from the person's age, intelligence and education. This deficiency materially impedes academic achievement or daily living."

Dyscalculia: definitions

UK National Numeracy Strategy, 2001:

"Dyscalculia is a condition that affects the ability to acquire arithmetical skills. Dyscalculic learners may have difficulty understanding simple number concepts, lack an intuitive grasp of numbers, and have problems learning number facts and procedures. Even if they produce a correct answer or use a correct method, they may do so mechanically and without confidence."

Dyscalculia: definitions

Mahesh Sharma, 1997

"Dyscalculia is an inability to conceptualise numbers, number relationships (arithmetical facts) and the outcomes of numerical operations (estimating the answer to numerical problems before actually calculating)."

Dyscalculia: definitions

Trott's working definition, 2006

"Dyscalculic students have a low level of numerical or mathematical competence compared to expectation. This expectation being based on unimpaired cognitive and language abilities and occurring within the normal range. The deficit will severely impede their academic progress or daily living. Dyscalculia is therefore an inability to effectively connect with number and mathematics."

Dyscalculia: definitions

Trott's working definition, 2006

"It may include difficulties recognising, reading, writing or conceptualising numbers, understanding numerical or mathematical concepts and their inter-relationships. It follows that dyscalculics may have difficulty with numerical operations, both in terms of understanding the process of the operation and in carrying out the procedure. Further difficulties may arise in understanding the systems that rely on this fundamental understanding, such as time, money, direction and more abstract mathematical, symbolic and graphical representations."

Dyscalculia

Dyscalculia mainly affects the ability to acquire arithmetical skills. It is characterised by difficulties with:

Conceptualisation of number and number relationships
Estimation

This can result in difficulties with learning number facts, acquiring arithmetic skills and learning mathematical procedures and often results in high levels of mathematical anxiety. Areas of relative strength might include any other cognitive and language abilities.

Areas of difficulty in mathematics

Problems with basic concepts
Difficulty seeing number inter-relationships
Very weak numerical and arithmetic skills
Difficulty recalling and using procedures with any confidence as often rote learnt with no understanding
Likely to be very anxious

Anxiety and resilience

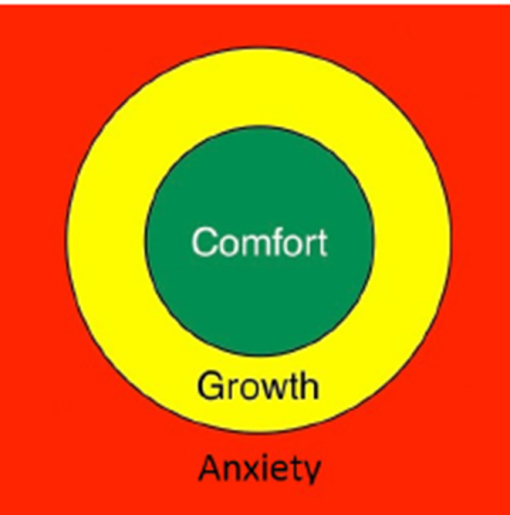
Three concentric circles. Inner circle coloured green and labelled comfort; middle circle coloured yellow and labelled growth; outer circle coloured red and labelled anxiety.

Maths Anxiety

Great work on this been done at Sheffield's maths support:

Maths anxiety is a situation-specific anxiety which can be described as "an emotion that blocks a person's reasoning ability when confronted with a mathematical situation" (Spicer, 2004).
Thought to primarily stem from negative learning experiences with maths in the past
Pain regions may be activated by thinking about maths
Maths is seen as a threat and triggers an anxiety response
Whilst someone is a state of anxiety, effective learning cannot occur so more negative experiences become likely

This can start a maths avoidance cycle

Maths Anxiety and SpLD

Working memory is important for solving mathematical problems
Anxiety interferes with working memory making maths seem harder than it is
Students with SpLD may have more limited working memory to start off with

Mathematical Resilience

Clare Lee and Sue Johnston-Wilder:

"Mathematical resilience describes a positive stance to learning that enables learners to engage successfully in what can be a difficult endeavour, that of learning mathematics. It is a pragmatic, mathematised understanding of the well-established concept resilience."

Mathematical Resilience

To be mathematically resilient a learner needs to:

understand through experience the need to struggle mathematically, learning mathematics can be difficult, but struggling and overcoming obstacles brings satisfaction with success
through experience believe that with effort and the right sort of help, that your ability to learn can grow and that what you can learn is not fixed or constrained in some way
have and use resources to support learning including friends, tutors, lecturers, maths support, textbooks and the wider community of mathematicians such as those available through the internet.

Mini needs assessment exercise

In groups consider the case study materials and

Try to capture the maths, statistics and numeracy challenges for the student in their context
You don't need to come up with recommendations at this point!

Technology, support methods and practical resources

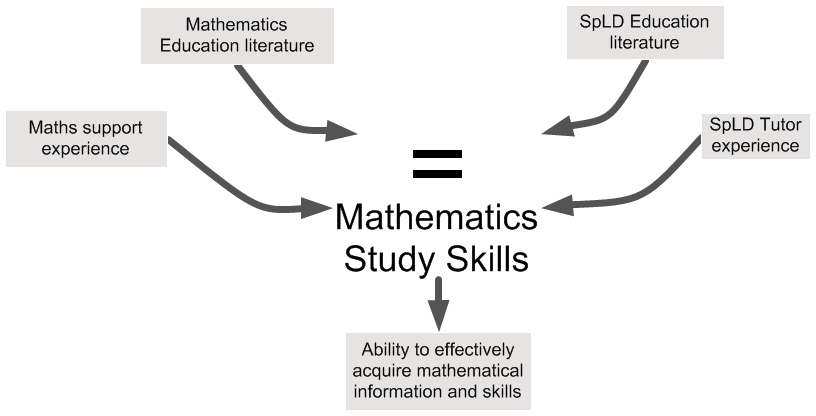
Diagram suggesting some of the inputs to mathematical study skills and the input of these to the ability to effectively acquire mathematical information and skills

What is my job?

Am I teaching numeracy or mathematical study skills?

Numeracy: 'I bring the math'. It is my job to design the mathematical activities.
Study skills: the student 'brings the math'. It is my job to enable the student to find ways of working.

The student identifies maths they are already comfortable with which we can use as an example.
For example, if we are looking at how to learn a process we work with a process they understand

My own mathematical resilience is important! I have to be comfortable with the student taking the mathematical lead.

General idea

Find student's comfort zone and move to zone of growth
Build up in manageable steps which do not trigger anxiety or which are designed to increase mathematical resilience, keep the student involved in planning this approach so they can measure progress
Watch for working memory overload and bring it to the student's awareness

Find approaches which reduce working memory load

Use concrete examples, concrete objects and visualisations
Use a structured multisensory approach with consistent colour and images

Example - Numeracy

The comfort zone for a student with dyscalculia may be very small. They might be comfortable adding in ones on their fingers and be able to recite the \(2\) and \(10\) times tables. They may not be able to place a number on the number line, may not understand place value, fractions, conversion between fraction and decimal, percentages etc.

Example - Numeracy

To start off with they may panic as soon as they see a formula, a list of numbers etc.
You need to create a careful series of growth zones.
These should build the connection between a concrete experience and what is written down.
Then go back the other way - start with what is written down and relate it back to an example concrete experience - draw pictures!

E.g. Pharmacuitical calculations

What the core mathematical skills?
Find a relevant concrete example
Build a series of growth zones and map this out for the student: First we are going to and so you will be able to, then we will...
Use relevant concrete multisensory experiences: bring in measures from the kitchen, orange juice, sugar, water - things you can see, taste and directly experience. Beads and other low tech can be used too. Record what you are doing with pictures. Start to bring in notation and words.

E.g. Statistical calculations

What the core mathematical skills?
Find a relevant concrete example
Build a series of growth zones and map this out for the student
Use relevant concrete multisensory experiences: Collect 8 leaves from the same tree, measure each; put them in size order; identify the mode and median (connect words to meaning); group within order and make a frequency plot; put leaves head to tail (sum of lengths), divide by 8 ('share' the length out in equal parts), make a paper leaf that size - this is the mean leaf; put 8 copies of the mean leaf head to tail - why does this leaf capture something useful? Start to bring in notation and words. Use consistant colour.

Example - maths study skills

An engineering student is happy with the maths as they learn it but over time starts to confuse processes.

It is not my job to teach them any of the processes.
It is my job to help them find a way of remembering processes and which one is which.
Teach how to make multisensory, structured summaries paired with concrete examples
Work with a process they are comfortable with and focus on extracting the key steps as a flow diagram, connect this to an illustrative example, use structured colour, add images, humour etc.

Accessing information

Recommend full notes prior to lectures

Accessible Word and web format which uses MathJax
Enable annotation and find methods for doing so

Encourage active mathematical reading

Slow the student down!
Consistent linking of symbol, word and process
Formation of self-explanations

Enable maths and surrounding English to be read aloud
Enable blocking out of information not in use, breaking up of large sections of text, changing of font, colour etc.

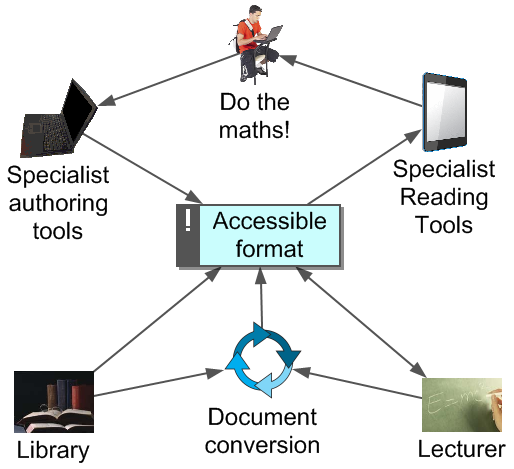
Lecturer and library must provide an accessible format or a format which can be converted. The student will require specialist reading tools which work with the format; tools which enable them to do and author maths, perhaps using a computer and so themselves produce a format which can be read by the lecturer.

A blurry photo of a blackboard containing mathematics

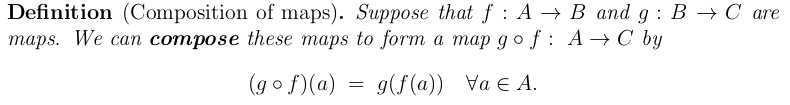
"[I am] struggling to make accurate notes during the lecture."
"Without the lecture notes there is no point in being there"
"The notes our lecturer uploads [...] are in hand-written format which I find extremely difficult to read"
"notes in text [...] would significantly facilitate my learning"
"My eyes don't especially like the font and it is all a bit close together."
"I often find my eye wanders around the page with some of the fonts that are used making it really difficult to follow what is being said/asked"
"I wondered if I could get some editable ones as theres lots of gaps and font size changes on the PDFs online which make it really hard when I'm trying to read them."
"Speech doesn’t work..."

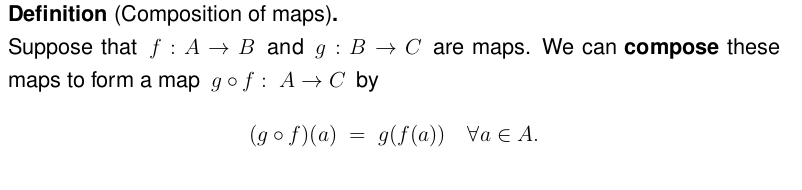
"The combination of notes I have prior to lectures and the narrative that lecturer add, enables me to determine words and equations written on the board."
"I have been finding them [clear print notes] much easier to read compared to other resources from lecturers"
"My plan is to print the [clear print] PDFs into OneNote which should enable me to annotate them during lectures"
"[It helps to] have notes and handouts laid out electronically, well-spaced out and so I can search within them using my computer"
"The clear print notes are incredibly useful."
"I would just like to say thank you. This service has been a great help over the last few years. Thank you very much for organising it and for providing quick help when it was needed."

Technology: flexible documents

Carefully authored mathematical documents can be adapted by a student and read aloud by appropriate technology.

Organising information

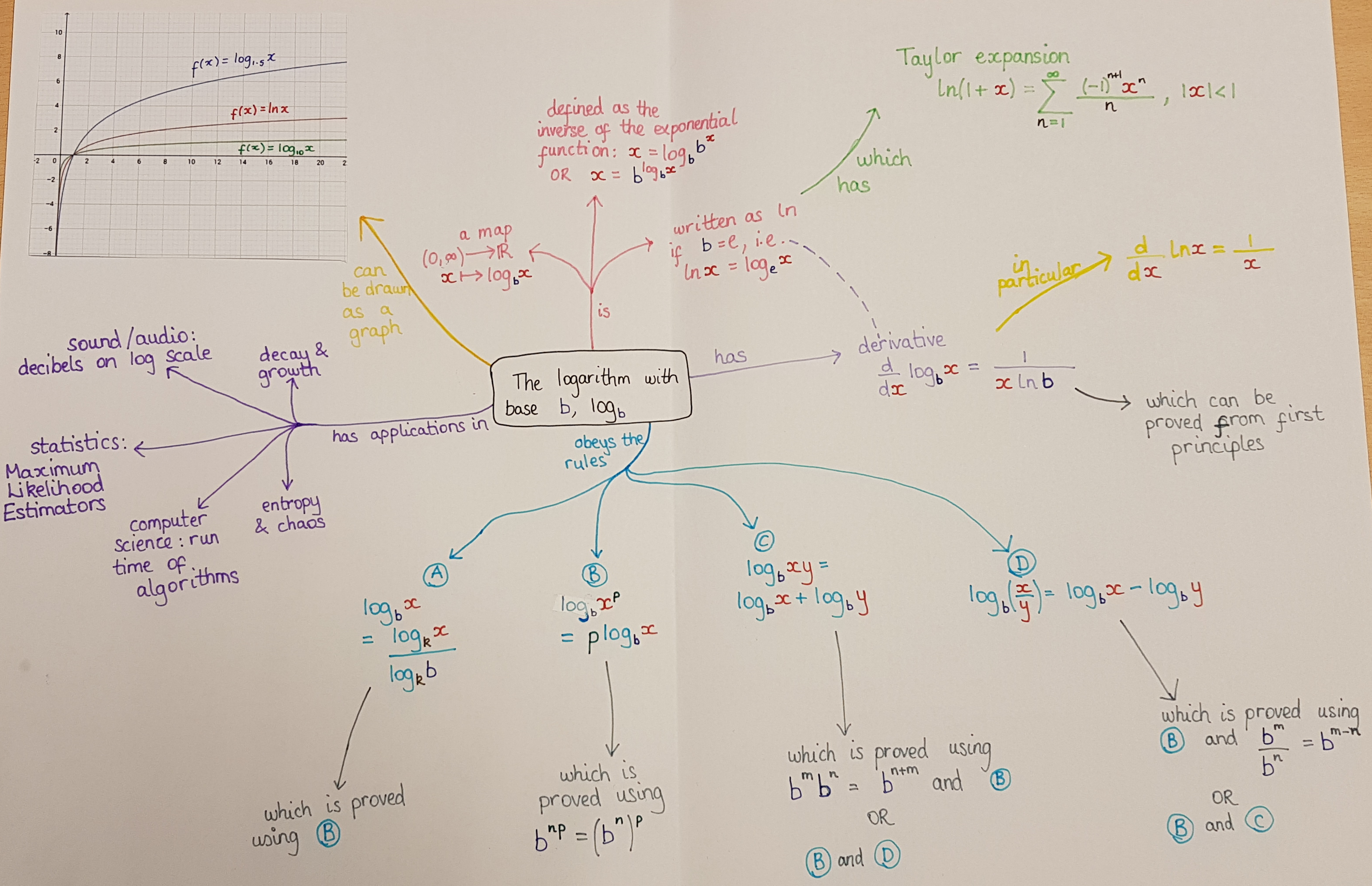
Enable making of flow charts and concept maps

To capture how concepts interlink
To capture how processes work
illustrated with images, using structured colour and connecting to concrete examples

Enable making of concept cards - capture the concept with examples
Enable making of template cards - capture a method with examples
Enable use of video and interactive resources

Memory

Encourage student to use multisensory approaches
Maintain connection with concrete memorable examples
Encourage overlearning and automaticity through practise e.g. apps and electronic quizes
Encourage metacognition, reflection on problem solving and production of templates, flow diagrams and maps

Technology: Overlearning

Structured colour

Many students use colour when they are writing mathematical notes but they often don't use it in a structured way. Structured colour supports making of links or keeps the same colour for the same operation e.g. from Matt Adereth and Stuart Riffle

\begin{equation*} \definecolor{energy}{RGB}{114,0,172} \definecolor{freq}{RGB}{45,177,93} \definecolor{spin}{RGB}{251,0,29} \definecolor{signal}{RGB}{18,110,213} \definecolor{circle}{RGB}{217,86,16} \definecolor{average}{RGB}{203,23,206} \color{energy} X_{\color{freq} k} \color{black} = \color{average} \frac{1}{N} \sum_{n=0}^{N-1} \color{signal}x_n \color{spin} e^{\mathrm{i} \color{circle} 2\pi \color{freq}k \color{average} \frac{n}{N}} \end{equation*}

To find the energy at a particular frequency, spin your signal around a circle at that frequency, and average a bunch of points along that path.

Flow diagrams

Concept image cards

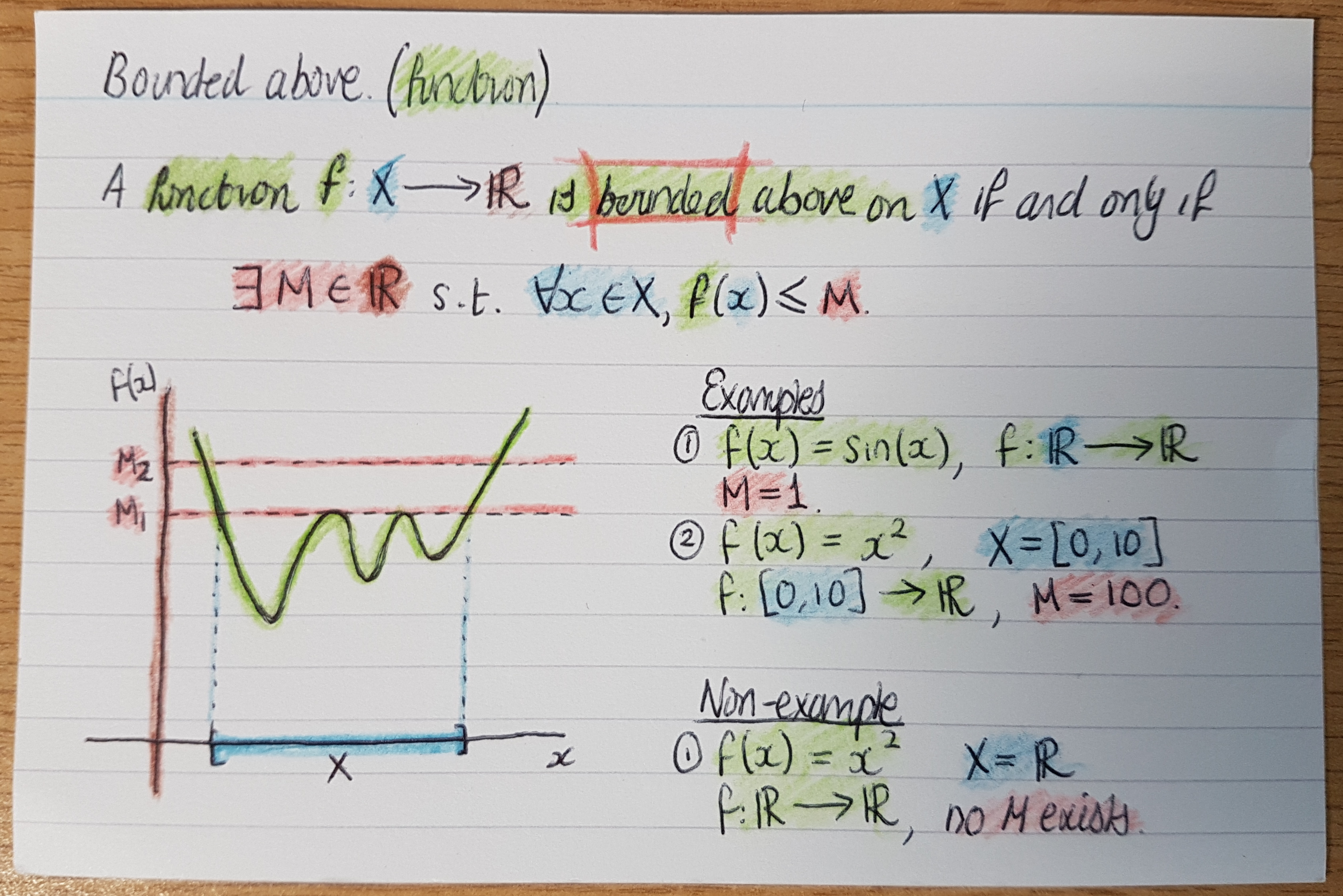
Theorem cards

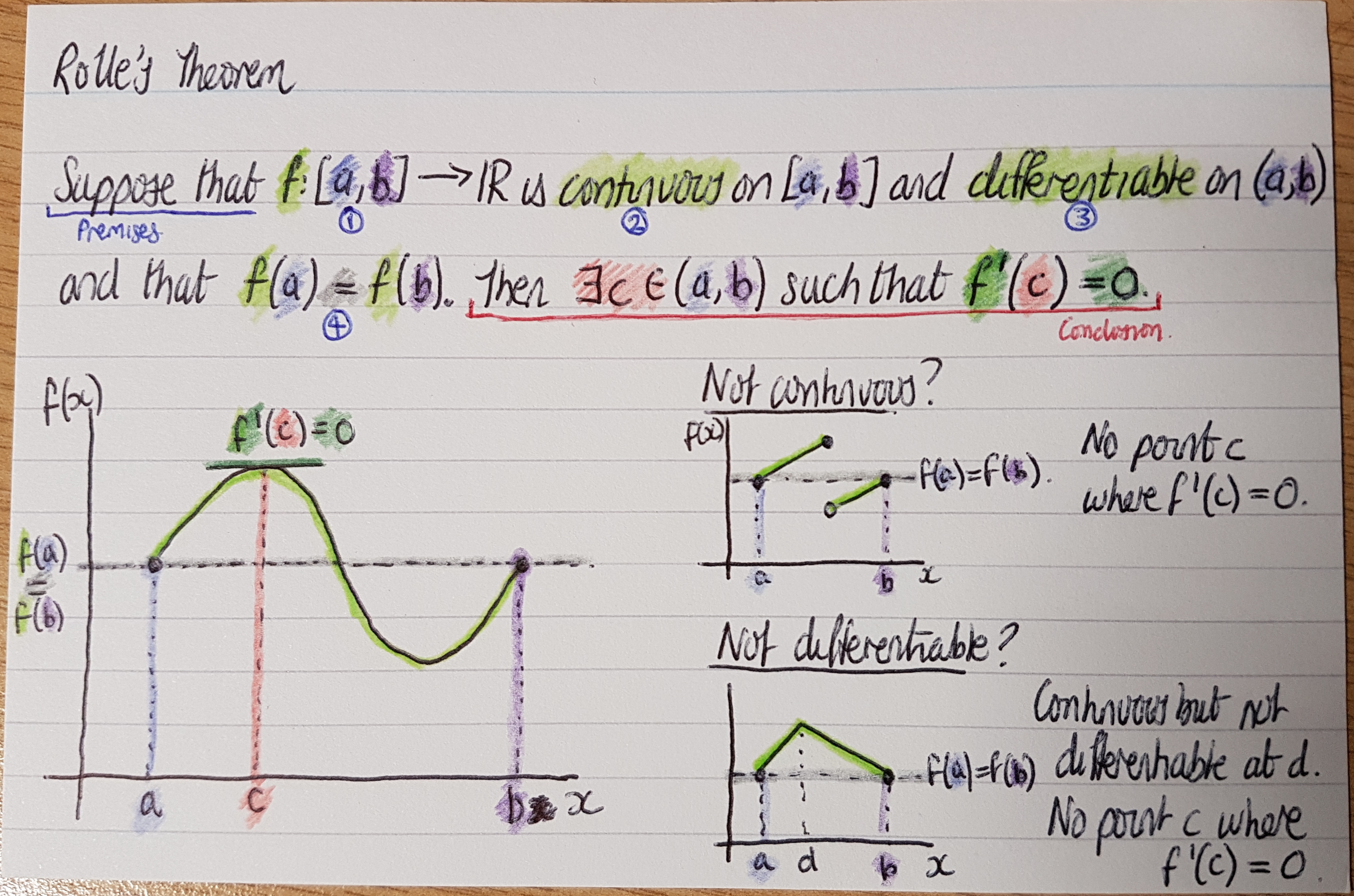
Concept mapping

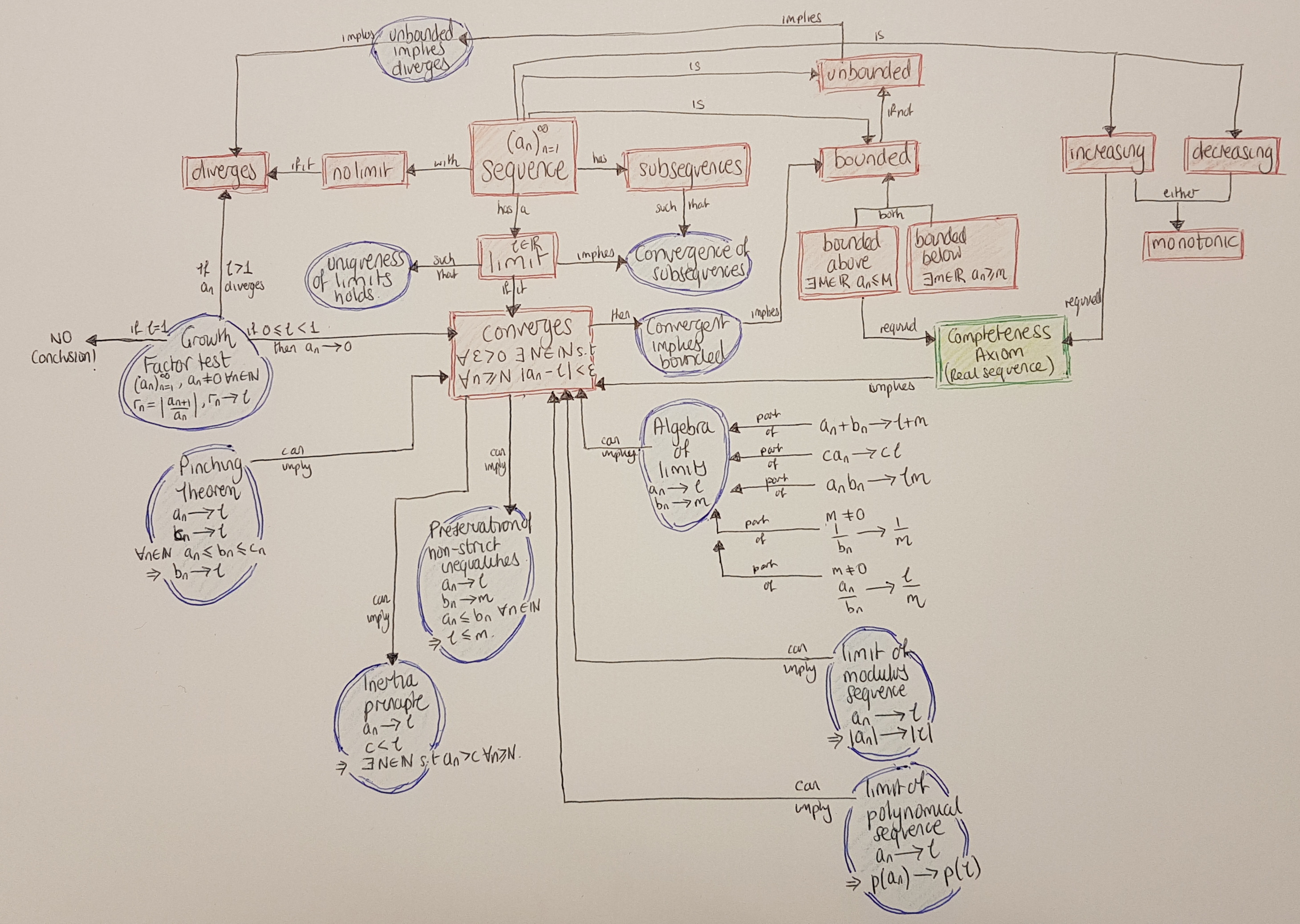
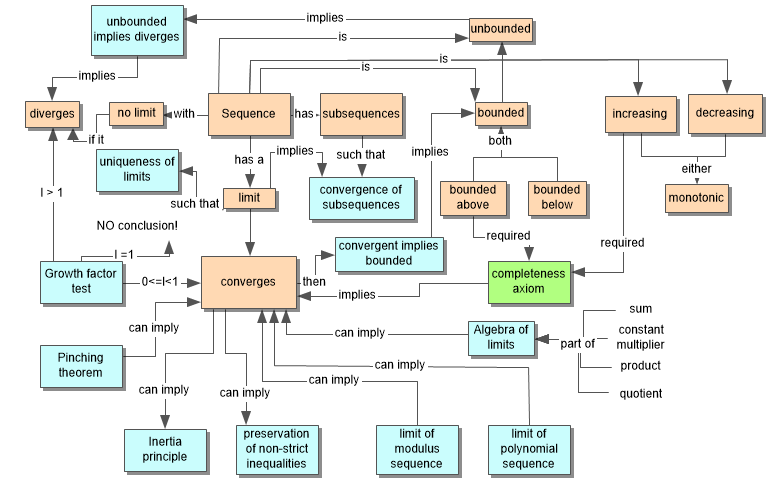
Technology: Concept mapping

Explain everything

Record tutorials, notes and annotations including handwriting, text, images, PDF, live websites and videos(!!) using Explain Everything

Describing a structured approach

Doing maths

Encourage drawing to capture what is going on
Encourage problem classification via templates
If stuck then work with a more concrete example and with actual objects
Encourage 'thinking aloud' and model it yourself, act as a scribe if needed
Encourage estimation and reflection on process - metacognition
Experiment with different ways to capture thought process

Technology: Low tech!

Technology: Visualisation

Technology: Effective equation input

Equatio and Read & Write

Collaboration?

Collaboration

Can we collaboratively design resources and approaches?

We need a collection of numeracy resources which cover material using relevant concrete multisensory experiences. Is this something we can put together nationally?
For study skills can we put together examples using a limited mathematical range?
Could these be explored as strategies in SpLD support?
Empowering students to bring them into maths support?
Then build on strategies into higher mathematical levels?

Where next?

Todo: Embedding of skills use into first year problem sheets
Done: Self access short course on mathematical study skills
Done: Supported access long course

Todo: Variant of course materials designed for use with general study skills tutors (constrained mathematical area) currently for DSA funded students only, students encouraged to follow up on using strategies in general mathematics support dropins.
Done: Referral to Mathematics Resource Centre group support if required. Students in these groups can access a limited amount of 1:1 support.

Todo: Specialist 1:1 mathematics study skills tutorials

Collaboration

If collaboration is important how do we achieve it? Locally? Nationally?

sigma Accessibility Special Interest Group (SIG): Join the mailing list, get involved... http://www.sigma-network.ac.uk/sigs/accessibility-sig
STEM Enable: Crowdsourcing for locating and sharing information to enable disabled students studying STEM subjects, http://stemenable.referata.com

Discussion: What is the aim?

In groups discuss the following and be ready to take part in a room wide discussion:

What are the boundaries on where specialist support should start and stop?
How should this work with more mainstream support at UWE?
What sorts of collaborations might bridge the gap?

Resources

Accessibility Special Interest Group

Feedback, questions and discussion

These slides are available at:
http://people.bath.ac.uk/cspehj/slides/SpLDMathsUWE/

My email address is:
E.H.Cliffe@bath.ac.uk

SpLDs and Maths

Bridging the Gap

Plan

Mind the gap!

SpLD support

Who does this?

How is it delivered?

Mathematics support...

Who does this?

How is it delivered?

A tension within maths support

Mind the gap!

SpLDs and mathematics

Neurodiversity...

Dyslexia and mathematics

The real fear

Dyslexia

Areas of difficulty in mathematics

Dyspraxia and mathematics

The real fear

Dyspraxia

Areas of difficulty in mathematics

Dyscalculia and mathematics

The real fear

Dyscalculia: definitions

Dyscalculia: definitions

Dyscalculia: definitions

Dyscalculia: definitions

Dyscalculia: definitions

Dyscalculia

Areas of difficulty in mathematics

Anxiety and resilience

Maths Anxiety and SpLD

Mini needs assessment exercise

Technology, support methods and practical resources

What is my job?

General idea

Example - Numeracy

Example - Numeracy

Example - maths study skills

Accessing information

Organising information

Memory

Structured colour

Flow diagrams

Concept image cards

Theorem cards

Concept mapping

Concept mapping

Technology: Concept mapping

Explain everything

Describing a structured approach

Doing maths

Technology: Low tech!

Equatio and Read & Write

Designing support exercise

Collaboration?

Collaboration

Where next?

Collaboration

Discussion: What is the aim?

Resources

Further reading

Feedback, questions and discussion