SpLDs and Maths Support
Bridging the Gap
Emma Cliffe
Plan
- SpLDs and mathematics
- Dyslexia
- Dyspraxia
- Dyscalculia
- Approaches and technology
- Bridging the gap?
- Collaboration and resources
SpLDs and mathematics
Neurodiversity...
is present when an exceptional degree of variation between neurocognitive processes results in noticeable and unexpected weaknesses in the performance of some everyday tasks when compared with much higher performances on a subset of measures of verbal and/or visual abilities for a given individual. These [...] include tasks of learning and remembering, time management, social interaction and attention span, as well as tasks requiring fine and gross motor movements
is a positive statement of differentiation
Grant, 2009. The psychological assessment of neurodiversity. Neurodiversity in higher education: Positive responses to specific learning differences, 33-62.
Dyslexia and mathematics
Maybe we could start by looking at some notes together?
Well, this important bit - what has it to do with conics?

That moment of maths support fear: I have no idea...
What led you to think about conics?
Well, it says so, right there: "conical form"
The real fear
I can resolve the current query but do I have the requisite knowledge and skills to support the student in building strategies for independence? Do I know what other difficulties the student might encounter?
Dyslexia
Dyslexia mainly affects the development of literacy and language related skills. It is characterised by difficulties with:
- Phonological processing
- Rapid naming
- Working memory
- Speed of visual processing
This can result in difficulties with reading, writing, spelling, sequencing and memory. Areas of relative strength might include, for example, verbal comprehension, visual reasoning, and holistic, rather than sequential, processing.
Areas of difficulty in mathematics
- Notes/solutions may contain copying errors, symbol confusion/reversals, word substitution or be incomplete
- Reading errors. Working memory may be overloaded when processing conceptually abstract or multi-step material
- Layout, font and style of "traditional" mathematics texts can add to processing difficulties
- Difficulty forming and retrieving association between mathematical vocabulary, notation and concept
- Difficulty learning, or producing from understanding, accurately stated definitions, theorems and formulae
- Combining multiple aspects and sequencing in procedures, arguments or proofs can be challenging
- May have difficulties moving from concrete to abstract
Dyspraxia and mathematics
Something my lecturer claimed about shapes makes no sense
Do you have a picture?
Apparently, this is cyclohexane in boat conformation
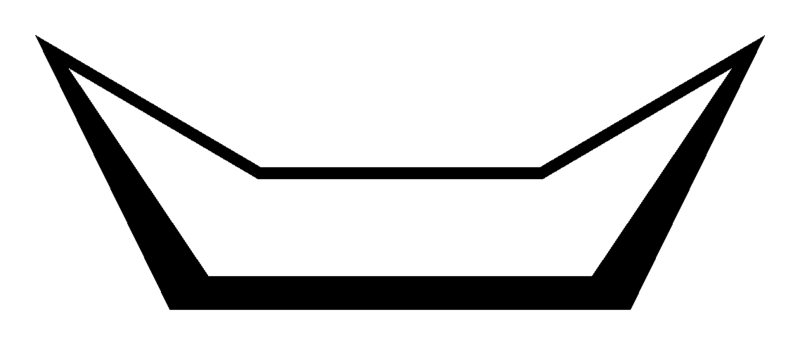
That moment of maths support fear as chemistry turns up
Can you see that it has the shape of a boat?
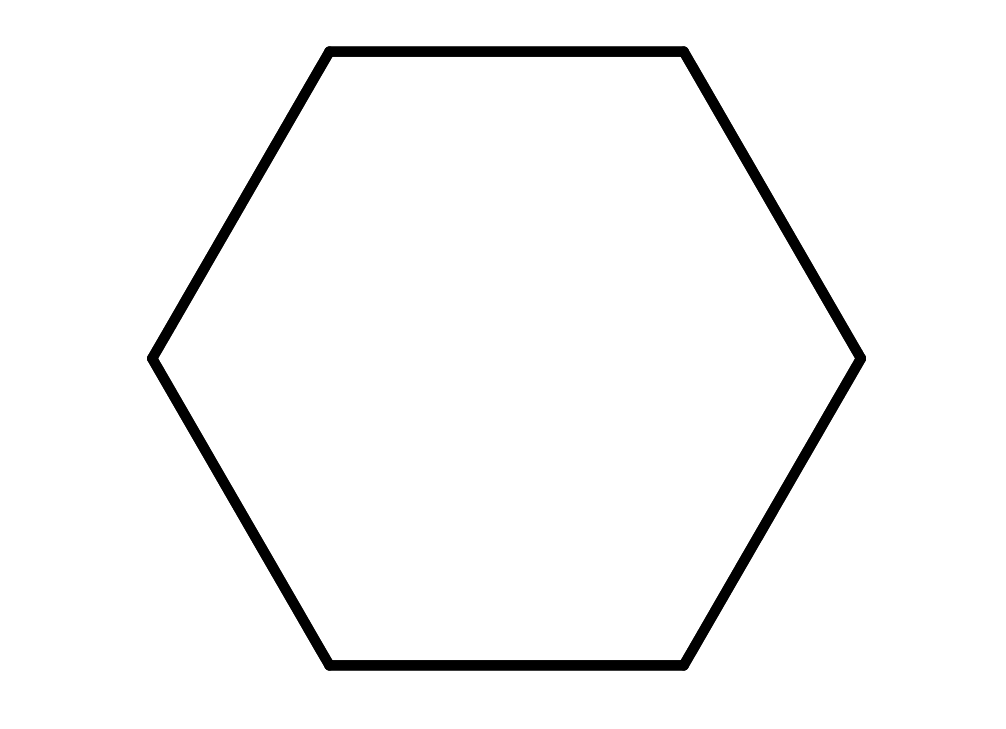
Yes, but cyclohexane is supposed to be a hexagon.
The real fear
I can resolve the current query but do I have the requisite knowledge and skills to support the student in building strategies for independence? Do I know what other difficulties the student might encounter?
Dyspraxia
Dyspraxia affects the planning of what you do and how you do it. It is associated with problems of perception, language and thought and is characterised by difficulties with:
- Motor coordination, including handwriting, drawing etc.
- Speed of visual processing
- Visual reasoning
- Working memory
This can result in difficulties with organisation, attention, spatial awareness, managing time and space, sequencing, memory and written expression. Areas of relative strength might include, for instance, verbal comprehension, verbal reasoning and 'out of the box' thinking.
Areas of difficulty in mathematics
- May have similar difficulties with processing speed and working memory as experienced by students with dyslexia but reading/spelling not specifically weak
- Spatial issues and weaker visual reasoning can have specific impacts e.g. geometry, concrete questions in 2D or 3D, seeing symmetry and structure
- Notetaking/solutions may be very difficult to read back, inaccurate and incomplete
- Drawings of figures etc. may be hard to follow
- May produce non-standard solutions
Dyscalculia and mathematics
I'm preparing for the Numeracy skills test and I need help. How do I know what to do with this question?

That moment of maths support fear: is there something in there to catch us out?
I see all the numbers, I become more and more anxious and I can't make any sense of it.
The real fear
I can resolve the current query but do I have the requisite knowledge and skills to support the student in building strategies for independence? Do I know what other difficulties the student might encounter?
Dyscalculia
Dyscalculia mainly affects the ability to acquire arithmetical skills. It is characterised by difficulties with:
- Conceptualisation of number and number relationships
- Estimation
This can result in difficulties with learning number facts, acquiring arithmetic skills and learning mathematical procedures and often results in high levels of mathematical anxiety. Areas of relative strength might include any other cognitive and language abilities.
Areas of difficulty in mathematics
- Problems with basic concepts
- Difficulty seeing number inter-relationships
- Very weak numerical and arithmetic skills
- Difficulty recalling and using procedures with any confidence as often rote learnt with no understanding
- Likely to be very anxious
Approaches and technology
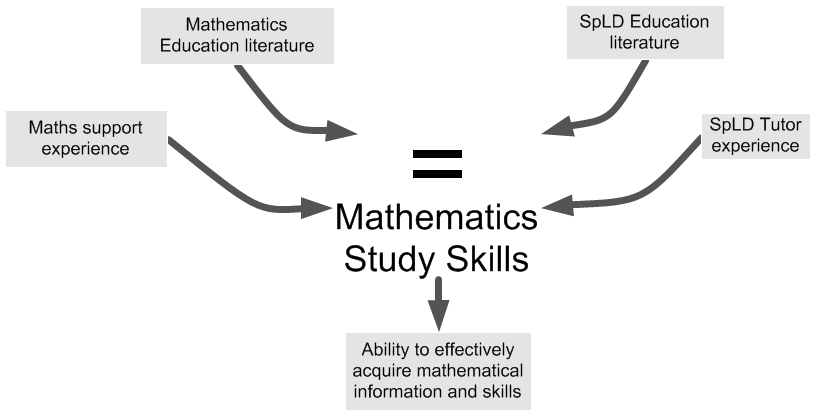
A tension within maths support
- In a rushed dropin it is hard for us to stand back from the presented maths problem
- The student expects that progress will be made on this
- In the long run the student is better served by building skills and strategies towards independent learning and problem solving - SpLD support is based on this premise
- But the student may not be receptive in this context
- This tension is an issue I will come back to...
Approaches: Thinking about our thinking
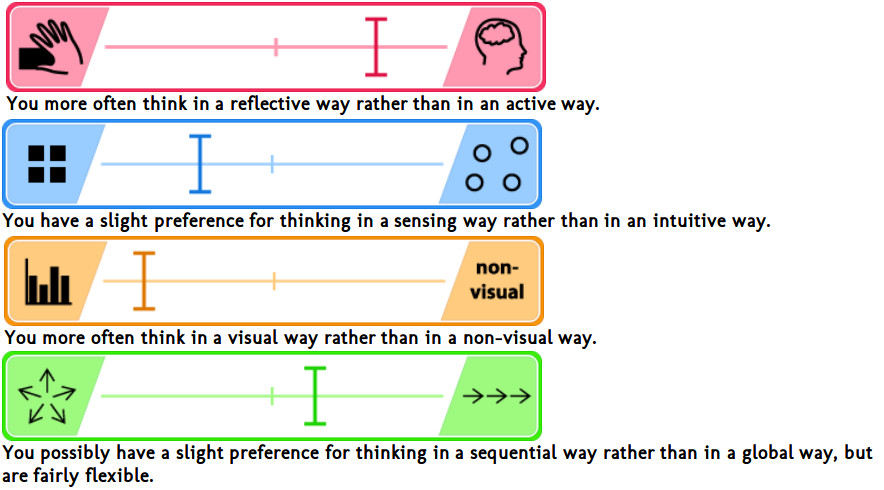
- Awareness of mathematical thinking styles helps us 'flex'
- Felder (1988) with 2002 preface might be a place to start.
Approaches: In the moment
- Use a multisensory approach with consistent 'structured' colour and images
- Consistently link symbol, word and process
- Break problems down into small, manageable steps
- Read maths aloud, 'think' aloud yourself
- Encourage thinking aloud, act as a scribe if needed
- Use visualisations, concrete examples and concrete objects
- Use flow charts, illustrated with images, using structured colour and connected to a concrete example
- Use concept maps, illustrated with images, using structured colour, highlighting relationships but also the connections between the abstract and the concrete
Approaches: In the moment
- Encourage student to use multisensory approaches
- Encourage overlearning e.g. index cards, electronic tests
- Encourage metacognition, reflection on problem solving
- Watch for working memory overload and bring it to the student's awareness
- Find alternative approaches which use different thinking styles or which reduce working memory load
- Block out information not in use, break up large sections of text, ensure student can change font, colour, have content read aloud if it helps
- Experiment with different ways to capture thought process and to write up work
Approaches: Building skills and strategies
- Notetaking for mathematics, structured annotation
- Using expanding symbol range and vocabulary
- Building rich accurate concept images, example use
- Connecting and mapping concepts, visualisation
- Active reading for mathematics, self-explanation
- Problem classification, structured problem solving
- Developing an internal monitor, raising metacognition
- Approaches for learning processes and algorithms, using diagrams, overlearning, achieving automaticity
- Approaches for learning concepts, producing proofs, from concept image/map to 'reproduction', memory and maths
- Mathematical writing skills, as appropriate to degree and level...
Technology: Low tech!



Technology: Handwriting+Audio on tablets
- Errors in handwritten notes can be corrected and so are less confusing - but don't rely on handwriting recognition for maths yet
- You and a student can record your conversion and handwritten notes on a document; you can create quick repeat-again-later resources this way too. We like Explain Everything but other apps may do the job.
- Students who talk aloud to facilitate their mathematical thought process but don't write down key things they say can use this to capture more of their process.
Technology: flexible documents
Carefully authored mathematical documents can be adapted by a student and read aloud by appropriate technology.
Technology: Concept mapping
Technology: Visualisation
Technology: Overlearning
Technology: Effective equation input
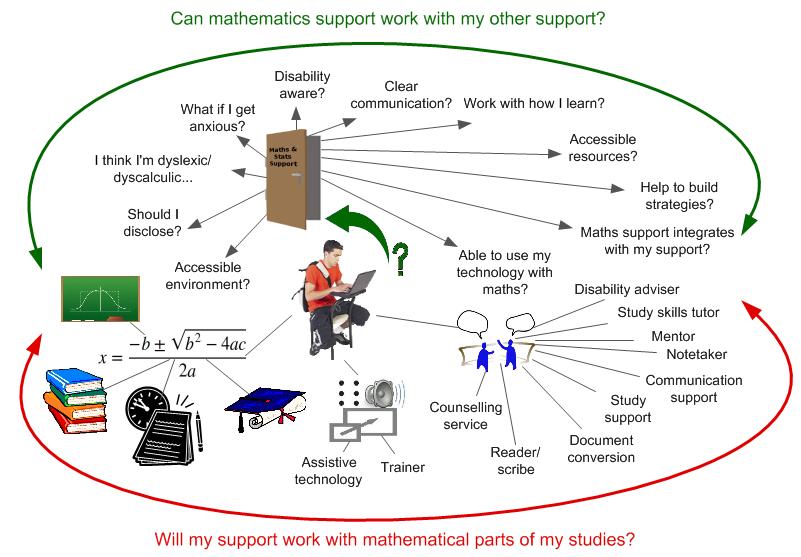
Bridging the gap?
SpLD support
This one to one support addresses the issues which some students might have in acquiring, recalling and retaining information in written and spoken language as well as the range of memory, organisational, attention and numeracy difficulties that students with specific learning differences often face when working in an HE context.
[...] This support should aim to develop students’ skills for autonomy in the learning environment. It should be tailored to a student’s individual needs [...]
SFE Non-Medical Help Services Reference Manual: http://www.practitioners.slc.co.uk/media/6192/non_medical_help_manual.pdf
Who does this?
Tutors hold membership of one of four professional bodies.
- Degree
- Recognised specialist Students with SpLD qualification
- Teaching experience
- Engagement with continuing professional development.
- Mathematical fluency and confidence highly varied.
How is it delivered?
- 1:1, perhaps weekly, perhaps for an extended period
- Planned with input from student, Educational Psychologist Report, Needs Assessment Report...
- Collaboratively build tailored approaches towards independence
Mathematics support...
... is a recognised collective term for extra-curricular mathematics and statistics teaching and learning services
[...] The term covers activities, facilities and/or resources provided to support and enhance students’ learning of mathematics or statistics
[...] It is designed to assist students in developing mathematical and/or statistical confidence and skills.
[...] students are encouraged to help themselves and not rely solely on the intervention of a tutor
sigma Network:
http://www.sigma-network.ac.uk/about/what-is-mathematics-statistics-support/
Who does this?
Staff with a mathematics background and varying levels of pedagogical knowledge and support experience:
- Teaching staff dedicated to the provision of extra-curricular maths support.
- Lecturers/Teaching Fellows as part of teaching load.
- Postgraduate tutors on casual basis.
- Knowledge of SpLD support highly varied.
How is it delivered?
- Dropin, workshops, group and 1:1 appointments
- Little tailored planning - tutor must often respond to, perhaps complex or poorly formed, queries immediately
- The student is there for maths help, often with a specific problem. Unpicking and responding to study skill gaps in real time is difficult and the student may not be receptive.
Mind the gap!
A student may not build effective and appropriate mathematics study skills for their degree.
Without which effectively acquiring mathematical information and skills independently is difficult.
Constant fire-fighting erodes confidence...
and may challenge a core identity of STEM students who "hated English but was good at maths and science".
Collaboration and resources
Collaboration
Can we collaboratively design resources and approaches?
- Using examples in a limited mathematical range?
- Could these be explored as strategies in SpLD support?
- Empowering students to bring them into maths support?
- Then build on strategies into higher mathematical levels?
Collaboration
If collaboration is important how do we achieve it? Locally? Nationally?
- sigma Accessibility Special Interest Group (SIG): Join the mailing list, get involved... http://www.sigma-network.ac.uk/sigs/accessibility-sig
- STEM Enable: Crowdsourcing for locating and sharing information to enable disabled students studying STEM subjects, http://stemenable.referata.com
Resources
Adams, Thomasenia Lott. 2003. Reading Mathematics: More than Words Can Say. The Reading Teacher 56 (8): 786–95.
Alcock, Lara. 2013. How to study for a mathematics degree. Oxford University Press.
Alock, Lara, Mark Hodds, and Matthew Inglis. 2014. Self-Explanation Training for Mathematics Students. Mathematics Education Centre, Loughborough University. Obtained via: http://www.lboro.ac.uk/departments/mec/research/mathematical-cognition/self-ex-training
Anthony, Glenda. 2015. When Mathematics Students Fail to Use Appropriate Learning Strategies. Mathematics Education Research Journal 8 (1): 23–37.
Brinkmann, Astrid. 2003. Graphical Knowledge Display - Mind Mapping and Concept Mapping as Efficient Tools in Mathematics Education. Mathematics Education Review, The Journal of Association of Mathematics Education Teachers 16: 39–48.
Cardelle-Elawar, Maria. 1992. Effects of Teaching Metacognitive Skills to Students with Low Mathematics Ability. Teaching and Teacher Education 8 (2): 109–21.
Chinn, S. J, and J. R Ashcroft. 2007. Mathematics for Dyslexics: Including Dyscalculia. 3rd ed. Whurr.
Houston, Kevin. 2009. How to Think Like a Mathematician. Cambridge University Press.
Resources
Kahn, Peter. 2001. Studying Mathematics and its Applications. Palgrave.
Mason, John, Leone Burton, and Kaye Stacey. 2010. Thinking Mathematically. 2nd ed. Pearson Education Limited.
Polya, G. 2014. How to Solve It: A New Aspect of Mathematical Method. Princeton University Press.
Schoenfeld, Alan H. 1992. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334-370). New York: MacMillan.
Shepherd, Mary D., and Carla C. van de Sande. 2014. Reading Mathematics for understanding - From Novice to Expert. The Journal of Mathematical Behavior 35 (September): 74–86.
Tall, David, and Shlomo Vinner. 1981. Concept Image and Concept Definition in Mathematics with Particular Reference to Limits and Continuity. Educational Studies in Mathematics 12 (2): 151–69.
Velleman, Daniel J. 2006. How to prove it: A structured approach. Cambridge University Press.
Vivaldi, Franco. 2014. Mathematical writing. Springer.
Williams, Carol G. 1998. Using Concept Maps to Assess Conceptual Knowledge of Function. Journal for Research in Mathematics Education 29 (4): 414–21.
Feedback, questions and discussion
These slides are available at:
http://people.bath.ac.uk/cspehj/slides/SpLDMathsABD/
My email address is:
E.H.Cliffe@bath.ac.uk

