The Verlet algorithm is one of the simplest of all integration algorithms, and was devised by L. Verlet in the early days of molecular simulation. It's simplicity and robustness made it the most popular algorithm for many years, though it is now superceded by its derivatives.

The equations of the algorithm are as follows.

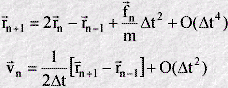
What do these equations mean? Well, assume we are at some point in the middle of a simulation - at a time step numbered n. At the start of this time step, we will know the positions of the atoms r_n, and their corresponding positions at the previous time step r_n-1. The first thing we must do is calculate the forces (f_n) acting on the atoms. We can then combine this information into the first equation, together with a suitable choice of time interval (Delta t), and calculate the the atom positions at the n+1th time step. (This equation is accurate to an order given by the fourth power of the time interval - which is indicated by the final term on the right of this equation.) Once we know the positions r_n+1 we can calculate the velocity (v_n) of each atom at time step n using the second equation, which is accurate to the second power of the time interval. When this is done we are ready to begin the next time step. Providing the time interval (Delta t) is small enough, this procedure is good enough to reveal all the interesting properties of the system!

Despite the simplicity of this algorithms, some aspects are unsatisfactory. Most obviously, the atom positions are given for the n+1th time step, while the velocities are given for the time step n, i.e. one time step behind. Also, it is apparent that we must store atom positions for three consecutive time steps if we wish to calculate the velocities as well. It is possible to derive variants of the Verlet algorithm which are free from these minor inconveniences.

The equations defining this algorithm are as follows:

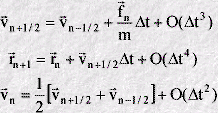
The algorithm defines velocities that are half a time step behind, or in front of, the current time step n. When the forces f_n of the current time step have been calculated, they are used in the first equation to advance the velocities from the half step behind n to the half step ahead. (In so doing the velocities can be seen to "leapfrog" over the current time step n, which is the origin of the algorithm's name.) When the atom velocities have been advanced, the positions can be updated using the second equation.

Throughout the computation of the atomic motion, the algorithm works with the half-step velocities. If the full-step velocities are required, the third equation may be used to obtain them. It is often adequate to work with the half-step velocities however.

The velocity Verlet algorithm provides both the atomic positions and velocities at the same instant of time, and for this reason may be regarded as the most complete form of Verlet algorithm. The basic equations are as follows:

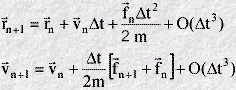
In practice these two equations are split further into three:

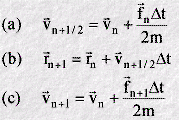
In this form the first equation (a) calculates a half-step velocity, using the force and velocity from time step n. This is sufficient to permit calculation of the atom positions at time step n+1, using equation (b). Finally, using the forces calculated from the new atomic position r_n+1, the half-step velocity is updated to the full step velocity v_n+1 (c). The advantage of this form of the velocity Verlet algorithm is that it requires less computer memory, because only one set of positions, forces and velocities need to be carried at any one time. This convenience is not apparent in the original equations.