Skip to:
Non-mathematical description
Basic mathematical description
My research
Going further
Return to main research page

Non-mathematical description

These descriptions are usually not entirely accurate, and sometimes not at all accurate. They're just stories, not mathematical descriptions.

Your house is made of bricks. For several reasons - price, insulation, weight - those bricks aren't solid pieces of rock - they're filled with tiny holes. Whoever makes the bricks has to be quite sure that when it rains, water can't seep through those holes - otherwise your house would get pretty wet inside. Percolation models ask questions like: how many holes can I put in my bricks (otherwise said, how cheap and lightweight can I make my bricks) without the inside of people's houses getting wet?
   Now think of the internet. It's a big network, with computers connected to other computers. I want my computer to be able to talk to pretty much every other computer on the internet very quickly. But my computer doesn't have a wire going from it to every other computer on the internet. That would need a lot of wires. I rely on the fact that there are enough wires going between pairs of computers around the world that it shouldn't be too hard to find a path of wires that connect my computer to any other computer.    You can think of each pair of computers that aren't connected by a wire as a hole in the brick. We like not having too many wires, because it costs money to have lots of wires. But we'd better make sure there are enough wires because otherwise it'll take too long for traffic to cross from my computer to my friend's computer, and Skype will tell us our connection isn't good enough for video.    So the percolation stuff that people studied a long time ago, because they didn't want their houses to get wet inside, looks like it might be useful for making sure I can talk to my friends on Skype. But bricks don't change much over the years, whereas the internet does. People are always plugging in wires and then unplugging them again. This is why we introduce dynamical percolation. Percolation that's always changing.

Basic mathematical description

These descriptions may contain some small inaccuracies in order to keep the discussion at a basic level.

Take the 2-dimensional square lattice Z^2. For each edge ij, flip a fair coin. If the coin comes up heads, colour the edge black. If it's tails, leave the edge white. (We can think of the black bits as holes in the brick.) One of the most famous results in probability theory is that the fair coin is critical here: if we had a slightly higer probability of heads, then there would be an infinite black cluster somewhere (in the brick terminology, there would be a good chance of having a hole running right through our brick).
   Now, for each edge independently, take an exponential random variable with mean 1, and after that amount of time, flip a new coin, and if it's heads, colour the edge black, if it's tails, colour it white. We don't care what colour it was before, we're completely rerandomising. Now take another independent exponential random variable with mean 1, wait that long again, and then rerandomise again. And repeat. So each edge in Z^2 is rerandomising independently at times that are decided by an independent Poisson process of intensity 1 (if you don't know what a Poisson process is, it's just what I said above: a string of times separated by independent exponential random variables).
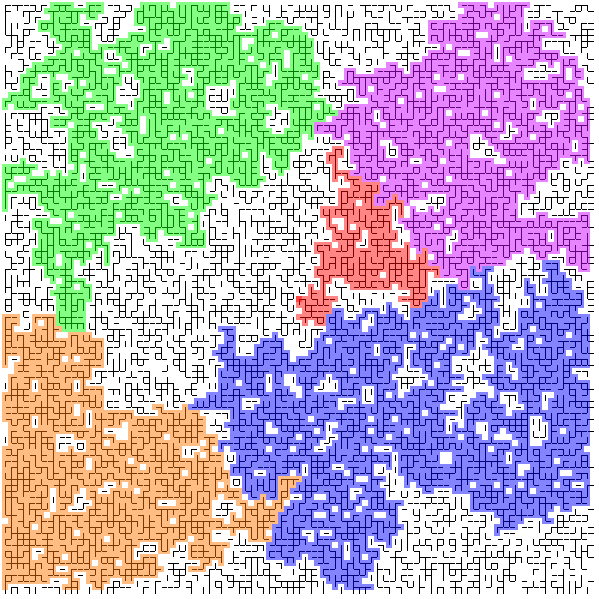
   At any fixed time, because we used fair coins, the probability of seeing an infinite black cluster is zero: the brick is waterproof. But there are uncountably many times, so it could still be that there exists a time in [0,infinity) when an infinite black cluster appears, and water gets through. We call these times "exceptional times". Are there exceptional times? If so then how many are there? What does the infinite black cluster look like at exceptional times?

Click the image below to see a simulation: here I've coloured five vertices in different colours, and their components take their colour (with some colours taking precedence over others if two coloured vertices are in the same component).

My research

Again, these descriptions may contain inaccuracies in order to keep the discussion at a basic level. If you want a precise discussion, then you'll have to read the papers!

Actually I don't have any research in this area. I can tell you a little bit about the questions above though. Yes, there are exceptional times. On the square lattice we don't know exactly how many there are. Well, there are infinitely many of course, but we don't know the Hausdorff dimension of the set. But if we work on the hexagonal lattice, the Hausdorff dimension of the set of exceptional times is 31/36. And if we make sense of the question properly, then "what does the infinite black cluster look like at exceptional times" can be answered by "it looks like a black cluster conditioned to have diameter at least r, when r goes to infinity" or something like that.
   If, like me, you find this stuff interesting, then you could do worse than to read Jeff Steif's survey on dynamical percolation. Or if you want some more details, then Christophe Garban and Jeff Steif's lecture notes on noise sensitivity and percolation, from their course at the Clay summer school that I went to in 2010, are very good too.

Going further

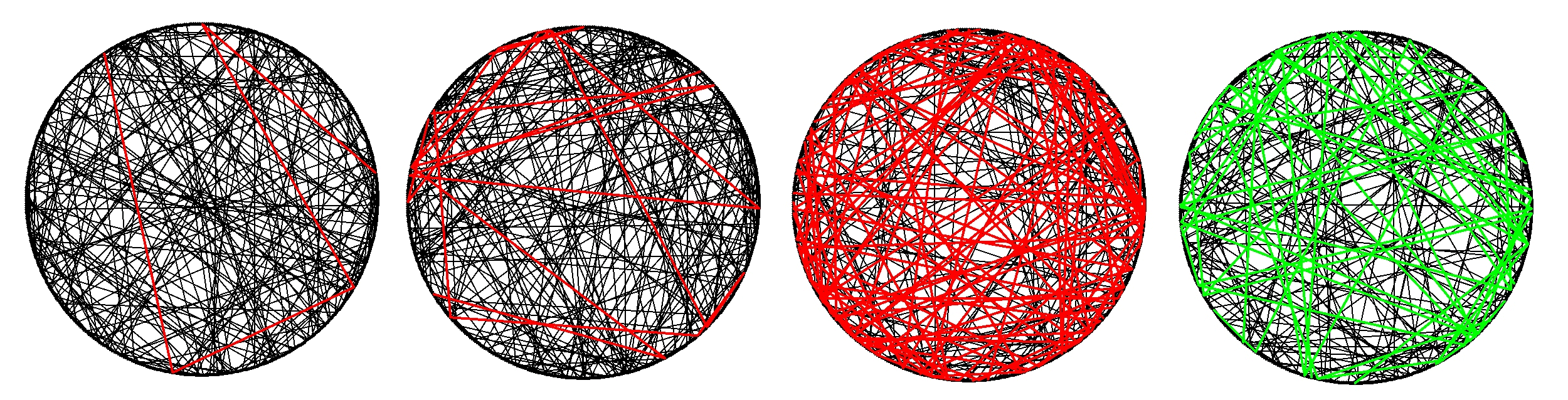
Of course there's no reason why we have to consider percolation only on lattices. In fact another of the most famous models in probability, the Erdös-Rényi random graph, is percolation on the complete graph with n vertices. If we choose the probability of heads to be p(n), then something interesting happens around p(n) = 1/n. If p(n) is a bit bigger than 1/n, then as n tends to infinity we see a "giant component": there are a constant times n vertices that are all connected to each other via black paths. If p(n) is a bit smaller than 1/n, then the largest component we see is of order log(n). If p(n) is very close to 1/n, then the largest component has size n^(2/3).
   Things are looking good: we have a phase transition, just like on the lattice. One problem is qualifying that precisely. On the lattice, we can just say "is there an infinite black component or not?" - but in our model we can't say "is there a giant component or not?" quite so easily because of the dependence on n. Fortunately there are ways around this. One way that I like is to ask "is vertex 1 connected to vertex 2?" - if p(n) is a bit bigger than 1/n then this happens with positive probability, but it never happens if p(n) is very close to 1/n. For some purposes, eg randomised algorithms, it might be better to ask "are two uniformly chosen vertices connected", but we're splitting hairs now. (As far as I know these characterisations of "giant component" are my own, although I haven't checked thoroughly - if you plan on using them please let me know!)
   As n tends to infinity, the critical Erdös-Rényi random graph has a scaling limit, which looks like a collection of continuum random trees with a few extra loops. Can we make sense of a scaling limit of the dynamical process where each edge is rerandomised at a certain rate, maybe depending on n? If so, what does it look like? If we get the rate right, then components should be joining together and splitting apart in a reasonable fashion, and we can hope that there might be exceptional times at which two uniformly chosen points are connected.

The image below shows some realisations of the Erdös-Rényi random graph. The component containing vertex 1 is coloured in red, unless it also contains vertex 2, in which case it's green. Click the image for a simulation of the dynamical process in action.